1.3. The Kibble mechanismn

The model described in the last subsection is an example in which the transition may be second-order. As we saw, for temperatures much larger than the critical one the vacuum expectation value of the scalar field vanishes at all points of space, whereas for T < T_c it evolves smoothly in time towards a non vanishing <| | >. Both thermal and quantum fluctuations influence the new value taken by <| | > and therefore it has no reasons to be uniform in space. This leads to the existence of domains wherein the <| () | > is coherent and regions where it is not. The consequences of this fact are the subject of this subsection.

Phase transitions can also be first-order proceeding via bubble nucleation. At very high energies the symmetry breaking potential has <| | > = 0 as the only vacuum state. When the temperature goes down to T_c a set of vacua, degenerate to the previous one, develops. However this time the transition is not smooth as before, for a potential barrier separates the old (false) and the new (true) vacua (see, e.g. Figure 1.1). Provided the barrier at this small temperature is high enough, compared to the thermal energy present in the system, the field will remain trapped in the false vacuum state even for small ( < T_c) temperatures. Classically, this is the complete picture. However, quantum tunneling effects can liberate the field from the old vacuum state, at least in some regions of space: there is a probability per unit time and volume in space that at a point a bubble of true vacuum will nucleate. The result is thus the formation of bubbles of true vacuum with the value of the field in each bubble being independent of the value of the field in all other bubbles. This leads again to the formation of domains where the fields are correlated, whereas no correlation exits between fields belonging to different domains. Then, after creation the bubble will expand at the speed of light surrounded by a `sea' of false vacuum domains. As opposed to second-order phase transitions, here the nucleation process is extremely inhomogeneous and <| () | > is not a continuous function of time.

Let us turn now to the study of correlation lengths and their rôle in the formation of topological defects. One important feature in determining the size of the domains where <| () | > is coherent is given by the spatial correlation of the field . Simple field theoretic considerations [see, e.g., Copeland, 1993] for long wavelength fluctuations of lead to different functional behaviors for the correlation function G(r) < (r₁) (r₂) >, where we noted r = |r₁ - r₂|. What is found depends radically on whether the wanted correlation is computed between points in space separated by a distance r much smaller or much larger than a characteristic length ^-1 = m(T) ^1/2 |<>|, known as the correlation length. We have

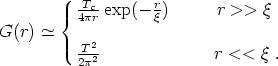
(3)

This tells us that domains of size ~ m^-1 arise where the field is correlated. On the other hand, well beyond no correlations exist and thus points separated apart by r >> will belong to domains with in principle arbitrarily different orientations of the Higgs field. This in turn leads, after the merging of these domains in a cosmological setting, to the existence of defects, where field configurations fail to match smoothly.

However, when T T_c we have m 0 and so , suggesting perhaps that for all points of space the field becomes correlated. This fact clearly violates causality. The existence of particle horizons in cosmological models (proportional to the inverse of the Hubble parameter H^-1) constrains microphysical interactions over distances beyond this causal domain. Therefore we get an upper bound to the correlation length as < H^-1 ~ t.

The general feature of the existence of uncorrelated domains has become known as the Kibble mechanism [Kibble, 1976] and it seems to be generic to most types of phase transitions.