


3.1. Goto-Nambu Strings
Our aim now is to introduce extra fields into the problem. The simple Lagrangian we saw in previous sections was a good approximation for ideal structureless strings, known under the name of Goto-Nambu strings [Goto, 1971; Nambu, 1970]. Additional fields coupled with the string-forming Higgs field often lead to interesting effects in the form of generalized currents flowing along the string core.
But before taking into full consideration the internal structure of
strings we will start by setting the scene with the simple Abelian
Higgs model (which describes scalar electrodynamics) in order to fix
the notation etc. This is a prototype of gauge field theory with
spontaneous symmetry breaking G = U(1)
 {1}. The
Lagrangian reads
[Higgs, 1964]
{1}. The
Lagrangian reads
[Higgs, 1964]
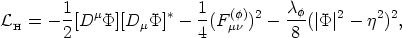
| (17) |
with gauge covariant derivative Dµ =
 µ +
i q
A(
µ +
i q
A( )µ, antisymmetric tensor
F(
)µ, antisymmetric tensor
F( )µ
)µ =
=
 µ
A(
µ
A( )
) -
-

 A(
A( )µ for the gauge vector field
A(
)µ for the gauge vector field
A( )
) ,
and complex scalar field
,
and complex scalar field
 =
|
=
| |ei
|ei with gauge coupling
q.
with gauge coupling
q.
The first solutions for this theory were found by Nielsen & Olesen [1973]. A couple of relevant properties are noteworthy:
 2.
For GUT local strings this gives µ ~ 1022g / cm,
while one finds µ ~
2.
For GUT local strings this gives µ ~ 1022g / cm,
while one finds µ ~
 2
ln(r / ms-1)
2
ln(r / ms-1)

 if strings are
global, due to the absence of compensating gauge fields. This
divergence is in general not an issue, because global strings only
in few instances are isolated; in a string network, a natural cutoff is the
distance to the neighboring string.
if strings are
global, due to the absence of compensating gauge fields. This
divergence is in general not an issue, because global strings only
in few instances are isolated; in a string network, a natural cutoff is the
distance to the neighboring string.

 1/2
1/2
 and
mv ~ q
and
mv ~ q
 , corresponding to
the inverse of the Compton wavelengths of the scalar (Higgs) and vector
(A(
, corresponding to
the inverse of the Compton wavelengths of the scalar (Higgs) and vector
(A( )
) )
particles, respectively.
)
particles, respectively.

 (1 / qr)
d
(1 / qr)
d / d
/ d
 for
r
for
r 
 .
.
After a closed path around the vortex one has
 (2
(2 ) =
) =
 (0),
which implies that the winding phase
(0),
which implies that the winding phase
 should be an integer
times the cylindrical angle
should be an integer
times the cylindrical angle
 , namely
, namely
 =
n
=
n .
This integer n is dubbed the `winding number'. In turn, from this
fact it follows that there exists a tube of quantized `magnetic' flux,
given by
.
This integer n is dubbed the `winding number'. In turn, from this
fact it follows that there exists a tube of quantized `magnetic' flux,
given by
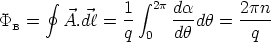
| (18) |
In the string there is a sort of competing effect between the fields:
the gauge field acts in a repulsive manner; the flux doesn't like to
be confined to the core and B lines repel each other. On the other
hand, the scalar field behaves in an attractive way; it tries to
minimize the area where
V( )
)
 0, that is, where the field
departs from the true vacuum.
0, that is, where the field
departs from the true vacuum.
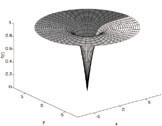
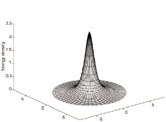
| 
|
Figure 1.6 Higgs field and energy
profiles for Goto-Nambu cosmic strings.
The left panel shows the amplitude of the Higgs field around the
string. The field vanishes at the origin (the false vacuum) and
attains its asymptotic value (normalized to unity in the figure) far
away from the origin. The phase of the scalar field (changing from 0
to 2 | |
Finally, we can mention a few condensed-matter `cousins' of
Goto-Nambu strings: flux tubes in superconductors
[Abrikosov, 1957]
for the nonrelativistic version of gauge strings
( corresponds
to the Cooper pair wave function). Also, vortices in superfluids, for the
nonrelativistic version of global strings
(
corresponds
to the Cooper pair wave function). Also, vortices in superfluids, for the
nonrelativistic version of global strings
( corresponds to the
Bose condensate wave function).
Moreover, the only two relevant scales of the problem we mentioned
above are the Higgs mass ms and the gauge vector mass
mv. Their inverse give an idea of the characteristic
scales on which
the fields acquire their asymptotic solutions far away from the string
`location'. In fact, the relevant core widths of the string are given
by ms-1 and
mv-1. It is the comparison of
these scales that draws the dividing line between two qualitatively
different types of solutions. If we define the parameter
corresponds to the
Bose condensate wave function).
Moreover, the only two relevant scales of the problem we mentioned
above are the Higgs mass ms and the gauge vector mass
mv. Their inverse give an idea of the characteristic
scales on which
the fields acquire their asymptotic solutions far away from the string
`location'. In fact, the relevant core widths of the string are given
by ms-1 and
mv-1. It is the comparison of
these scales that draws the dividing line between two qualitatively
different types of solutions. If we define the parameter
 =
(ms / mv)2,
superconductivity theory
says that
=
(ms / mv)2,
superconductivity theory
says that  < 1 corresponds to Type I behavior while
< 1 corresponds to Type I behavior while
 > 1
corresponds to Type II. For us,
> 1
corresponds to Type II. For us,
 < 1
implies that the characteristic scale for the vector field is smaller
than that for the Higgs field and so magnetic field B flux lines are
well confined in the core; eventually, an n-vortex string with high
winding number n stays stable. On the contrary,
< 1
implies that the characteristic scale for the vector field is smaller
than that for the Higgs field and so magnetic field B flux lines are
well confined in the core; eventually, an n-vortex string with high
winding number n stays stable. On the contrary,
 > 1 says that
the characteristic scale for the vector field exceeds that for the
scalar field and thus B flux lines are not confined;
the n-vortex string will eventually split into n vortices
of flux
2
> 1 says that
the characteristic scale for the vector field exceeds that for the
scalar field and thus B flux lines are not confined;
the n-vortex string will eventually split into n vortices
of flux
2 /q. In summary:
/q. In summary:
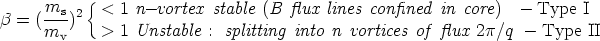
| (19) |