


3.5. The dual formalism
The usual procedure for treating a specific cosmic string dynamical
problem consists in writing and varying an action which is assumed to
be the integral over the worldsheet of a Lagrangian function depending
on the internal degrees of freedom of the worldsheet. In particular,
for the structureless string, this is taken to be the Goto-Nambu
action, i.e. the integral over the surface of the constant string
tension. In more general cases, various functions have been suggested
that supposedly apply to various microscopic field
configurations. They share the feature that the description is
achieved by means of a scalar function
 , identified with the
phase of a physical field trapped on the string, whose squared
gradient, namely the state parameter w, has values which completely
determine the dynamics through a Lagrangian function
, identified with the
phase of a physical field trapped on the string, whose squared
gradient, namely the state parameter w, has values which completely
determine the dynamics through a Lagrangian function
 (w). This
description has the pleasant feature that it is easily
understandable, given the clear physical meaning of
(w). This
description has the pleasant feature that it is easily
understandable, given the clear physical meaning of
 . However, as we shall
see, there are instances for which it
is not so easily implemented and for which an alternative, equally
valid, dual formalism is better adapted [Carter, 1989].
. However, as we shall
see, there are instances for which it
is not so easily implemented and for which an alternative, equally
valid, dual formalism is better adapted [Carter, 1989].
Macroscopic equation of state
But first, let us concentrate on the macroscopic equation of state. At this point, it is clear that conducting strings have a considerably richer structure than Goto-Nambu strings. In particular, Witten strings have and internal structure with its own equation of state U = U(T). This, in turn, allows us to compute the characteristic perturbations speeds [Carter, 1989] :
Of course, these characteristic speeds are not defined for a structureless Goto-Nambu string, but are fully meaningful for any other model. Numerical results for Witten strings by Peter [1992] yield cL < cT, i.e. the regime is supersonic.
We will now explore the different ansätze proposed in the literature over the years. Clearly, the simplest case is that one without any currents, namely the Goto-Nambu action. In the present formalism it is expressed by the action
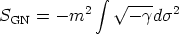
| (43) |
which is proportional to string worldsheet area. The corresponding
Lagrangian is given simply by
 GN =
-m2 and its
equation of state results U = T = m2.
GN =
-m2 and its
equation of state results U = T = m2.
The first thing that comes to the mind when trying to extend this
simple action to the case including currents is of course to add a
small (linear) term proportional to the state parameter w, which
itself includes the relevant information on the currents. Hence, a
first try would be
 linear =
-m2 - w / 2. It turns out that
this simple model is also self-dual (with
linear =
-m2 - w / 2. It turns out that
this simple model is also self-dual (with
 linear
= -m2 -
linear
= -m2 -
 / 2], to be precised below)
and the equation of state resulting is (for both electric and magnetic
regimes)
U + T = 2m2. However, it follows that
cT < cL = 1, i.e., the
model is subsonic and this goes at odds with the numerical
results for Witten strings.
/ 2], to be precised below)
and the equation of state resulting is (for both electric and magnetic
regimes)
U + T = 2m2. However, it follows that
cT < cL = 1, i.e., the
model is subsonic and this goes at odds with the numerical
results for Witten strings.
2nd try: keeping with minimal modifications autour the
Goto-Nambu solution, another, Kaluza-Klein inspired, model was
proposed:  KK
= -m[m2 + w]1/2. This model
is also self-dual and the resulting equation of state is UT =
m4. Moreover,
in the limit of small currents it reproduces the linear model of the
last paragraph. However, this time both characteristic perturbation
speeds are equal and smaller than unity, cT =
cL < 1, i.e. the model is transonic
and this fact disqualifies it for modeling Witten strings.
KK
= -m[m2 + w]1/2. This model
is also self-dual and the resulting equation of state is UT =
m4. Moreover,
in the limit of small currents it reproduces the linear model of the
last paragraph. However, this time both characteristic perturbation
speeds are equal and smaller than unity, cT =
cL < 1, i.e. the model is transonic
and this fact disqualifies it for modeling Witten strings.
At this point, one may think that there is an additional relevant
parameter in the theory, the scale associated with the
current-carrier mass, which we shall note
m* (=
m ). It is
only by introducing this extra mass scale that the precise numerical
solutions for Witten strings can be recovered. Two models were
proposed, the first one with
). It is
only by introducing this extra mass scale that the precise numerical
solutions for Witten strings can be recovered. Two models were
proposed, the first one with
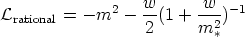
| (44) |
for which we get the amplitude of the
 -condensate
-condensate
 -1 =
(1 + (w / m2*))-2
(recall that it was
-1 =
(1 + (w / m2*))-2
(recall that it was
 -1
-1

 dx dy
|
dx dy
| |2
and C
|2
and C  |w|1/2
|w|1/2
 dx dy
|
dx dy
| |2).
This ansatz fits well the w
|2).
This ansatz fits well the w
 -m2
-m2 divergence in
the macroscopic charge density C [see
Figure (1.8)] and it is the best
choice for spacelike currents.
divergence in
the macroscopic charge density C [see
Figure (1.8)] and it is the best
choice for spacelike currents.
The second model is given by
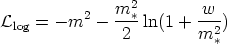
| (45) |
and we get  -1
= (1 + w /
m2*)-1. This one is the
best for timelike currents and is OK for spacelike currents as well
[Carter & Peter,
1995].
-1
= (1 + w /
m2*)-1. This one is the
best for timelike currents and is OK for spacelike currents as well
[Carter & Peter,
1995].
These two two-scale models we will employ below to study the dynamics of conducting string loops and the influence of electromagnetic self-corrections on this dynamics at first order between the current and the self-generated electromagnetic field. But before that, let us introduce the formal framework we need for the job.
The dual formalism
Here we will derive in parallel expressions for the currents and state
parameters in two representations, which are dual to each other. This
will not be specific to superconducting vacuum vortex defects, but is
generally valid to the wider category of elastic string models
[Carter, 1989].
In this formalism one works with a two-dimensional
worldsheet supported master function
 (
( ) considered as the
dual of
) considered as the
dual of  (w),
these functions depending respectively on the
squared magnitude of the gauge covariant derivative of the scalar
potentials
(w),
these functions depending respectively on the
squared magnitude of the gauge covariant derivative of the scalar
potentials  and
and
 as given by
as given by
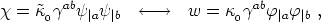
| (46) |
where  0 and
0 and
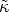 0 are adjustable,
respectively positive and negative, dimensionless normalization
constants that, as we will see below, are related to each other.
The arrow in the previous equation stands to mean an exact
correspondence between quantities appropriate to each dual
representation.
0 are adjustable,
respectively positive and negative, dimensionless normalization
constants that, as we will see below, are related to each other.
The arrow in the previous equation stands to mean an exact
correspondence between quantities appropriate to each dual
representation.
In Eq. (46) the scalar potentials
 and
and
 are such that their
gradients are orthogonal to each other, namely
are such that their
gradients are orthogonal to each other, namely
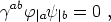
| (47) |
implying that if one of the gradients, say
 |a is
timelike, then the other one, say
|a is
timelike, then the other one, say
 |a, will
be spacelike,
which explains the different signs of the dimensionless constants
|a, will
be spacelike,
which explains the different signs of the dimensionless constants
 0
and
0
and 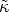 0.
0.
Whether or not background electromagnetic and gravitational fields are
present, the dynamics of the system can be described in the two
equivalent dual representations which are
governed by the master function
 and the
Lagrangian scalar
and the
Lagrangian scalar
 , that are functions
only of the state parameters
, that are functions
only of the state parameters
 and
w, respectively. The corresponding conserved current vectors,
na
and za, in the worldsheet, will be given according to the
Noetherian prescription
and
w, respectively. The corresponding conserved current vectors,
na
and za, in the worldsheet, will be given according to the
Noetherian prescription
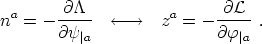
| (48) |
This implies
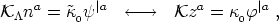
| (49) |
where we use the induced metric for internal index raising, and where
 and
and

 can be written as
can be written as
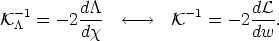
| (50) |
As it will turn out, the equivalence of the two mutually dual descriptions is ensured provided the relation
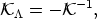
| (51) |
holds. This means one can define
 in two alternative ways,
depending on whether it is seen it as a function of
in two alternative ways,
depending on whether it is seen it as a function of
 or of
or of
 .
We shall therefore no longer use the function
.
We shall therefore no longer use the function 
 in what follows.
in what follows.
Based on Eq. (47) that expresses the orthogonality of the
scalar potentials we can conveniently write the relation between
 and
and
 as follows
as follows
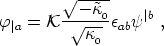
| (52) |
where  is the
antisymmetric surface measure tensor (whose square is the induced metric,
is the
antisymmetric surface measure tensor (whose square is the induced metric,
 ab
ab
 bc =
bc =
 ac).
From this and using Eq. (46) we
easily get the relation between the state variables,
ac).
From this and using Eq. (46) we
easily get the relation between the state variables,
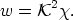
| (53) |
Both the master function
 and the Lagrangian
and the Lagrangian
 are
related by a Legendre type transformation that gives
are
related by a Legendre type transformation that gives
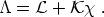
| (54) |
The functions  and
and
 can be seen
[Carter, 1997] to
provide values for the energy per unit length U and the tension
T of the string depending on the signs of the state parameters
can be seen
[Carter, 1997] to
provide values for the energy per unit length U and the tension
T of the string depending on the signs of the state parameters
 and w. (Originally, analytic forms for these functions
and w. (Originally, analytic forms for these functions
 and
and  were derived as
best fits to the eigenvalues of the
stress-energy tensor in microscopic field theories). The necessary
identifications are summarized in Table 1.2.
were derived as
best fits to the eigenvalues of the
stress-energy tensor in microscopic field theories). The necessary
identifications are summarized in Table 1.2.
| Equations of state for both regimes | ||||
| regime | U | T |  and w and w | current |
| electric | - | - | < 0 | timelike |
| magnetic | - | - | > 0 | spacelike |
This way of identifying the energy per unit length and tension with
the Lagrangian and master functions also provides the constraints on
the validity of these descriptions: the range of
variation of either w or
 follows from the requirement of
local stability, which is equivalent to the demand that the squared
speeds cE2 = T / U
and cL2 = -dT / dU of
extrinsic and longitudinal (sound type) perturbations be
positive. This is thus characterized by the unique relation
follows from the requirement of
local stability, which is equivalent to the demand that the squared
speeds cE2 = T / U
and cL2 = -dT / dU of
extrinsic and longitudinal (sound type) perturbations be
positive. This is thus characterized by the unique relation
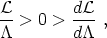
| (55) |
which should be equally valid in both the electric and magnetic ranges. Having defined the internal quantities, we now turn to the actual dynamics of the worldsheet and prove explicitly the equivalence between the two descriptions.
Equivalence between  and
and

The dynamical equations for the string model can be
obtained either from the master function
 or from the
Lagrangian
or from the
Lagrangian  in the
usual way, by applying the variation
principle to the surface action integrals
in the
usual way, by applying the variation
principle to the surface action integrals
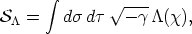
| (56) |
and
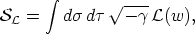
| (57) |
(where 
 det{
det{ ab}) in which the independent variables are
either the
scalar potential
ab}) in which the independent variables are
either the
scalar potential  or the
phase field
or the
phase field  on the
worldsheet
and the position of the worldsheet itself, as specified by the
functions xµ{
on the
worldsheet
and the position of the worldsheet itself, as specified by the
functions xµ{ ,
,  }.
}.
Independently of the detailed form of the complete system, one knows in advance, as a consequence of the local or global U(1) phase invariance group, that the corresponding Noether currents will be conserved, namely
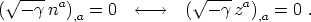
| (58) |
For a closed string loop, this implies (by Green's theorem) the conservation of the corresponding flux integrals
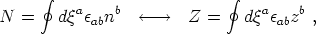
| (59) |
meaning that for any circuit round the loop one will obtain the same value for the integer numbers N and Z, respectively. Z is interpretable as the integral value of the number of carrier particles in the loop, so that in the charge coupled case, the total electric charge of the loop will be Q = Ze. Moreover, the angular momentum of the closed loop turns out to be simply J = Z N.
The loop is also characterized by a second independent integer number N whose conservation is trivially obvious. Thus we have the topologically conserved numbers defined by
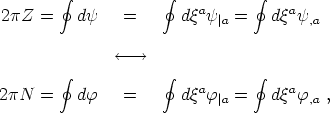
| (60) |
where it is clear that N, being related to the phase of a physical
microscopic field, has the meaning of what is usually referred to as
the winding number of the string loop. The last equalities in
Eqs. (60) follow just from explicitly writing the covariant
derivative |a and noting that the circulation integral
multiplying Aµ vanishes. Note however that,
although Z and N
have a clearly defined meaning in terms of underlying microscopic
quantities, because of Eqs. (59) and (60), the roles of
the dynamically and topologically conserved integer numbers are
interchanged depending on whether we derive our equations from
 or from its dual
or from its dual
 .
.
As usual, the stress momentum energy density distributions
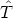
 µ
µ and
and 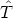
 µ
µ on the background
spacetime are derivable from the action by varying the actions with
respect to the background metric, according to the specifications
on the background
spacetime are derivable from the action by varying the actions with
respect to the background metric, according to the specifications
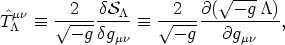
| (61) |
and
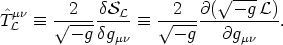
| (62) |
This leads to expressions of the standard form, i.e. expressible as an integral over the string itself
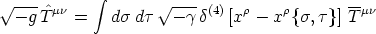
| (63) |
in which the surface stress energy momentum tensors on the worldsheet (from which the surface energy density U and the string tension T are obtainable as the negatives of its eigenvalues) can be seen to be given by
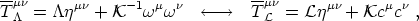
| (64) |
where the (first) fundamental tensor of the worldsheet is given by
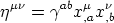
| (65) |
and the corresponding rescaled currents
 µ and
cµ are obtained by setting
µ and
cµ are obtained by setting
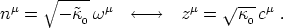
| (66) |
Plugging Eqs. (66) into Eqs. (64), and using Eqs. (51), (53) and (54), we find that the two stress-energy tensors coincide:
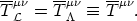
| (67) |
This is indeed what we were looking for since the dynamical equations for the case at hand, namely
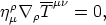
| (68) |
which hold for the uncoupled case, are then strictly
equivalent whether we start with the action
S or with
S
or with
S .
.
Inclusion of Electromagnetic Corrections
Implementing electromagnetic corrections
[Carter, 1997b],
even at the
first order, is not an easy task as can already be seen by the much
simpler case of a charged particle for which a mass renormalization is
required even before going on calculating anything in effect related
to electromagnetic field. The same applies in the current-carrying
string case, and the required renormalization now concerns the master
function  . However,
provided this renormalization is
adequately performed, inclusion of electromagnetic corrections, at
first order in the coupling between the current and the
self-generated electromagnetic field, then becomes a very simple
matter of shifting the equation of state, everything else being left
unchanged. Let us see how this works explicitly.
. However,
provided this renormalization is
adequately performed, inclusion of electromagnetic corrections, at
first order in the coupling between the current and the
self-generated electromagnetic field, then becomes a very simple
matter of shifting the equation of state, everything else being left
unchanged. Let us see how this works explicitly.
Defining Kµ



 µ
µ







 the second fundamental
tensor of the
worldsheet, the equations of motion of a charge coupled string read
the second fundamental
tensor of the
worldsheet, the equations of motion of a charge coupled string read
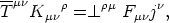
| (69) |
where 
 µ is
the tensor of orthogonal projection to the worldsheet
(
µ is
the tensor of orthogonal projection to the worldsheet
(
 µ
= g
µ
= g µ
-
µ
- 
 µ),
Fµ
µ),
Fµ =
2
=
2 [µ
A
[µ
A ]
is the external electromagnetic tensor and jµ
stands for the electromagnetic current flowing along the string, namely
in our case
]
is the external electromagnetic tensor and jµ
stands for the electromagnetic current flowing along the string, namely
in our case
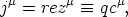
| (70) |
with r the
effective charge of the current carrier in unit of the electron charge
e (working here in units where e2
 1/137).
1/137).
Before going on, let us explain a bit the last equations. The above
Eq. (69) is no other than an extrinsic equation of motion
that governs the evolution of the string worldsheet in the presence of
an external field. In fact we readily recognize the external force
density acting on the worldsheet
f = F
= F µ jµ, just
a Lorentz-type force with jµ the corresponding
surface current.
µ jµ, just
a Lorentz-type force with jµ the corresponding
surface current.
Let us also give a simple example where the above seemingly
complicated equation of motion proves to be something very well known
to all of us. In fact, the above is the two-dimensional analogue of
Newton's second law. For a point particle of mass m the Lagrangian
is  = -m, which
implies that its stress energy momentum tensor
is given by
= -m, which
implies that its stress energy momentum tensor
is given by 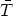 µ
µ = m uµ
u
= m uµ
u (with uµ uµ = -1, for the
unit tangent vector uµ of the particle's
worldline). Then, the first fundamental tensor is
(with uµ uµ = -1, for the
unit tangent vector uµ of the particle's
worldline). Then, the first fundamental tensor is
 µ
µ = - uµ
u
= - uµ
u . From this
it follows that the second fundamental tensor can be constructed, giving
Kµ
. From this
it follows that the second fundamental tensor can be constructed, giving
Kµ
 = uµ
u
= uµ
u
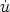
 . Hence, the extrinsic equation of motion yields
m
. Hence, the extrinsic equation of motion yields
m
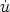
 =
= 
 µ
fµ, i.e., the external to the
worldline force
µ
fµ, i.e., the external to the
worldline force 
 µ fµ being
equal to the mass times the acceleration
[Carter, 1997b].
µ fµ being
equal to the mass times the acceleration
[Carter, 1997b].
As we mentioned, we are now interested in Eq. (69) which is the natural generalization to two dimensions of Newton's second law. But now we want to include self interactions. The self interaction electromagnetic field on the worldsheet itself can be evaluated [Witten, 1985] and one finds
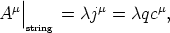
| (71) |
with
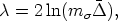
| (72) |
where 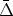 is an
infrared cutoff scale to compensate for the
asymptotically logarithmic behavior of the electromagnetic potential
and m
is an
infrared cutoff scale to compensate for the
asymptotically logarithmic behavior of the electromagnetic potential
and m the ultraviolet cutoff corresponding to the effectively
finite thickness of the charge condensate, i.e., the Compton
wavelength of the current-carrier
m
the ultraviolet cutoff corresponding to the effectively
finite thickness of the charge condensate, i.e., the Compton
wavelength of the current-carrier
m -1. In the practical situation of
a closed loop,
-1. In the practical situation of
a closed loop,
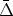 should at
most be taken as the total length of the loop.
should at
most be taken as the total length of the loop.
The contribution of the self field of Eq. (71) in the equations of motion (69) was calculated by Carter [1997b] and the result is interpretable as a renormalization of the stress energy tensor. That is, the result including electromagneti�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������c corrections is recovered if, in Eq. (61), one uses
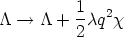
| (73) |
instead of  . So,
electromagnetic corrections are simply
taken into account in the dual formalism employing the master function
. So,
electromagnetic corrections are simply
taken into account in the dual formalism employing the master function
 (
( )
unlike the case if we used
)
unlike the case if we used
 (w). In fact, it
is not always possible to invert the above relation to get an
appropriate replacement for the Lagrangian. That the correction
enters through a simple modification of
(w). In fact, it
is not always possible to invert the above relation to get an
appropriate replacement for the Lagrangian. That the correction
enters through a simple modification of
 (
( ) and not of
) and not of
 (w) is
understandable if one remembers that
(w) is
understandable if one remembers that
 is the
amplitude of the current, so that a perturbation in the
electromagnetic field acts on the current linearly, so that an
expansion in the electromagnetic field and current yields, to first
order in q,
is the
amplitude of the current, so that a perturbation in the
electromagnetic field acts on the current linearly, so that an
expansion in the electromagnetic field and current yields, to first
order in q, 

 +
1/2 jµ
Aµ, which transforms easily into Eq. (73).
+
1/2 jµ
Aµ, which transforms easily into Eq. (73).
One example of the implementation of the above formalism is the study of circular conducting cosmic string loops [Carter, Peter & Gangui, 1997]. In fact, the mechanics of strings developed above allows a complete study of the conditions under which loops endowed with angular momentum will present an effective centrifugal potential barrier. Under certain conditions, this barrier will prevent the loop collapse and, if saturation is avoided, one would expect that loops will eventually radiate away their excess energy and settle down into a vorton type equilibrium state.
If this were the whole story then we would of course be in a big problem, for these vortons, as stable objects, would not decay and would most probably be too abundant to be compatible with the standard cosmology. It may however be possible that in realistic models of particle physics the currents could not survive subsequent phase transitions so that vortons could dissipate. Another way of getting rid of (at least some of) the excess of abundance of these objects is to take account of the electromagnetic self interactions in the macroscopic state of the conducting string: as we said above, the electromagnetic field in the vicinity of the string will interact with the very same string current that generated it, with the resulting effect of modifying its macroscopic equation of state (see Figure 1.9). These modifications make a departure of the resulting vorton distribution from that expected otherwise, diminishing their relic abundance.
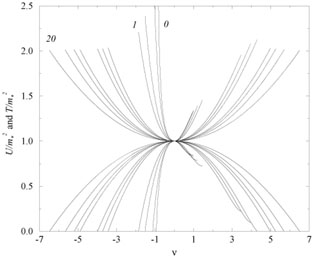
|
Figure 1.9. Variation of the equation of
state with the electromagnetic self-correction
|