


5.4. CMB polarization
The possibility that the CMB be polarized was first discussed by
Martin Rees in 1968, in the context of anisotropic Universe models.
In spite of his optimism, and after more than thirty years, there is
still no positive detection of the polarization field.
Unlike the BOOMERANG  Œ
[G experiment, MAP will have the capability to
detect it and this to a level of better than 10 µK in its low
frequency channels. Polarization is an important probe both for
cosmological models and for the more recent history of our nearby
Universe. It arises from the interactions of CMB photons with free
electrons; hence, polarization can only be produced at the last
scattering surface (its amplitude depends on the duration of
the decoupling process) and, unlike temperature fluctuations, it is
unaffected by variations of the gravitational potential after
last scattering. Future measurements of polarization will thus
provide a clean view of the inhomogeneities of the Universe at about
400,000 years after the Bang.
Œ
[G experiment, MAP will have the capability to
detect it and this to a level of better than 10 µK in its low
frequency channels. Polarization is an important probe both for
cosmological models and for the more recent history of our nearby
Universe. It arises from the interactions of CMB photons with free
electrons; hence, polarization can only be produced at the last
scattering surface (its amplitude depends on the duration of
the decoupling process) and, unlike temperature fluctuations, it is
unaffected by variations of the gravitational potential after
last scattering. Future measurements of polarization will thus
provide a clean view of the inhomogeneities of the Universe at about
400,000 years after the Bang.
For understanding polarization, a couple of things should be
clear. First, the energy of the photons is small compared to the mass
of the electrons. Then, the CMB frequency does not change, since the
electron recoil is negligible. Second, the change in the CMB
polarization (i.e., the orientation of the oscillating electric field
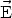 of the radiation)
occurs due to
a certain transition, called Thomson scattering. The transition
probability per unit time is proportional to a combination of the old
(
of the radiation)
occurs due to
a certain transition, called Thomson scattering. The transition
probability per unit time is proportional to a combination of the old
(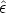 in
in ) and
new (
) and
new (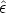 out
out ) directions of polarization in the form
|
) directions of polarization in the form
|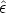 in
in ·
·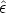 out
out |2. In other words, the initial direction
of polarization will be favored. Third, an oscillating
|2. In other words, the initial direction
of polarization will be favored. Third, an oscillating
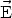 will push the electron to also oscillate; the latter can then be seen
as a dipole (not to be confused with the CMB dipole), and dipole
radiation emits preferentially perpendicularly to the direction of
oscillation. These `rules' will help us understand why the CMB
should be linearly polarized.
will push the electron to also oscillate; the latter can then be seen
as a dipole (not to be confused with the CMB dipole), and dipole
radiation emits preferentially perpendicularly to the direction of
oscillation. These `rules' will help us understand why the CMB
should be linearly polarized.
Previous to the recombination epoch, the radiation field is
unpolarized. In unpolarized light the electric field can be
decomposed into the two orthogonal directions (along, say,
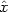 and
and  perpendicular to the
line of propagation (
perpendicular to the
line of propagation (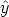 ). The
electric field along
). The
electric field along
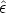 in
in (suppose
(suppose
 is vertical) will make
the electron oscillate also
vertically. Hence, the dipolar radiation will be maximal over the
horizontal xy-plane. Analogously, dipole radiation due to the
electric field along
is vertical) will make
the electron oscillate also
vertically. Hence, the dipolar radiation will be maximal over the
horizontal xy-plane. Analogously, dipole radiation due to the
electric field along 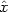 will
be on the yz-plane. If we now look from the side (e.g., from
will
be on the yz-plane. If we now look from the side (e.g., from
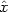 , on the horizontal plane and
perpendicularly to the incident direction
, on the horizontal plane and
perpendicularly to the incident direction
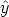 ) we will see a
special kind of scattered radiation. From our position we cannot
perceive the radiation that the electron oscillating along the
) we will see a
special kind of scattered radiation. From our position we cannot
perceive the radiation that the electron oscillating along the
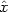 direction would emit,
just because this radiation goes to the
yz-plane, orthogonal to us. Then, it is as if only the
vertical
component (
direction would emit,
just because this radiation goes to the
yz-plane, orthogonal to us. Then, it is as if only the
vertical
component (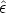 in
in ) of the incoming electric
field would cause the radiation we perceive. From the above rules we
know that the highest probability for the polarization of the outgoing
radiation
) of the incoming electric
field would cause the radiation we perceive. From the above rules we
know that the highest probability for the polarization of the outgoing
radiation 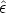 out
out will be to be aligned with
the incoming one
will be to be aligned with
the incoming one
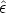 in
in , and therefore it
follows that the outgoing radiation will be linearly polarized.
Now, as both the chosen incoming direction and our position as
observers were arbitrary, the result will not be modified if we change
them. Thomson scattering will convert unpolarized radiation into
linearly polarized one.
, and therefore it
follows that the outgoing radiation will be linearly polarized.
Now, as both the chosen incoming direction and our position as
observers were arbitrary, the result will not be modified if we change
them. Thomson scattering will convert unpolarized radiation into
linearly polarized one.
This however is not the end of the story. To get the total effect we need to consider all possible directions from which photons will come to interact with the target electron, and sum them up. We see easily that for an initial isotropic radiation distribution the individual contributions will cancel out: just from symmetry arguments, in a spherically symmetric configuration no direction is privileged, unlike the case of a net linear polarization which would select one particular direction.
Fortunately, we know the CMB is not exactly isotropic; to the millikelvin precision the dominant mode is dipolar. So, what about a CMB dipolar distribution ? Although spatial symmetry does not help us now, a dipole will not generate polarization either. Take, for example, the radiation incident onto the electron from the left to be more intense than the radiation incident from the right, with average intensities above and below (that's a dipole); it then suffices to sum up all contributions to see that no net polarization survives. However, if the CMB has a quadrupolar variation in temperature (that it has, first discovered by COBE, to tens of µK precision) then there will be an excess of vertical polarization from left- and right-incident photons (assumed hotter than the mean) with respect to the horizontal one from top and bottom light (cooler). From any point of view, orthogonal contributions to the final polarization will be different, leaving a net linear polarization in the scattered radiation.
Within standard recombination models the predicted level of linear
polarization on large scales is tiny (see
Figure 1.17):
the quadrupole generated in the radiation distribution as the photons
travel between successive scatterings is too small. Multiple
scatterings make the plasma very homogeneous and only wavelengths that
are small enough (big  's) to
produce anisotropies over the
(rather short) mean free path of the photons will lead to a
significant quadrupole, and thus also to polarization. Indeed, if the
CMB photons last scattered at z ~ 1100, the SCDM model with
h = 1
predicts no more than 0.05 µK on scales greater than a few
degrees. Hence, measuring polarization represents an experimental
challenge. There is still no positive detection and the best upper
limits a few years ago were around 25 µK, obtained by Edward
Wollack and collaborators in 1993, and now improved to roughly
10µK on subdegree angular scales by
Hedman, et al., [2001]
(20).
's) to
produce anisotropies over the
(rather short) mean free path of the photons will lead to a
significant quadrupole, and thus also to polarization. Indeed, if the
CMB photons last scattered at z ~ 1100, the SCDM model with
h = 1
predicts no more than 0.05 µK on scales greater than a few
degrees. Hence, measuring polarization represents an experimental
challenge. There is still no positive detection and the best upper
limits a few years ago were around 25 µK, obtained by Edward
Wollack and collaborators in 1993, and now improved to roughly
10µK on subdegree angular scales by
Hedman, et al., [2001]
(20).
However, CMB polarization increases remarkably around the degree-scale
in standard models. In fact, for
 < 1° a bump with
superimposed acoustic oscillations reaching ~ 5 µK is
generically forecasted. On these scales, like for the temperature
anisotropies, the polarization field shows acoustic
oscillations. However, polarization spectra are sharper: temperature
fluctuations receive contributions from both density (dominant) and
velocity perturbations and these, being out of phase in their
oscillation, partially cancel each other. On the other hand,
polarization is mainly produced by velocity gradients in the
baryon-photon fluid before last scattering, which also explains why
temperature and polarization peaks are located differently. Moreover,
acoustic oscillations depend on the nature of the underlying
perturbation; hence, we do not expect scalar acoustic sound-waves in
the baryon-photon plasma, propagating with characteristic adiabatic
sound speed cs ~ c /
< 1° a bump with
superimposed acoustic oscillations reaching ~ 5 µK is
generically forecasted. On these scales, like for the temperature
anisotropies, the polarization field shows acoustic
oscillations. However, polarization spectra are sharper: temperature
fluctuations receive contributions from both density (dominant) and
velocity perturbations and these, being out of phase in their
oscillation, partially cancel each other. On the other hand,
polarization is mainly produced by velocity gradients in the
baryon-photon fluid before last scattering, which also explains why
temperature and polarization peaks are located differently. Moreover,
acoustic oscillations depend on the nature of the underlying
perturbation; hence, we do not expect scalar acoustic sound-waves in
the baryon-photon plasma, propagating with characteristic adiabatic
sound speed cs ~ c /
 3, close to that of an ideal
radiative fluid, to produce the same peak-frequency as that produced
by gravitational waves, which propagate with the speed of light c
(see Fig. 1.17).
3, close to that of an ideal
radiative fluid, to produce the same peak-frequency as that produced
by gravitational waves, which propagate with the speed of light c
(see Fig. 1.17).
The main technical complication with polarization (characterized by a tensor field) is that it is not invariant under rotations around a given direction on the sky, unlike the temperature fluctuation that is described by a scalar quantity and invariant under such rotations. The level of linear polarization is conveniently expressed in terms of the Stokes parameters Q and U. It turns out that there is a clever combination of these parameters that results in scalar quantities (in contrast to the above noninvariant tensor description) but with different transformation properties under spatial inversions (parity transformations). Then, inspired by classical electromagnetism, any polarization pattern on the sky can be separated into `electric' (scalar, unchanged under parity transformation) and `magnetic' (pseudo-scalar, changes sign under parity) components (E- and B-type polarization, respectively).
CMB polarization from global defects
One then expands these different components in terms of spherical
harmonics, very much like we did for temperature anisotropies, getting
coefficients am for E and B polarizations and, from these,
the multipoles CE,B
for E and B polarizations and, from these,
the multipoles CE,B . The interesting thing is that
(for symmetry reasons) scalar-density perturbations will not
produce any B polarization (a pseudo-scalar), that is
CB(S)
. The interesting thing is that
(for symmetry reasons) scalar-density perturbations will not
produce any B polarization (a pseudo-scalar), that is
CB(S) = 0. We see then that an unambiguous detection of some
level of B-type fluctuations will be a signature of the existence (and
of the amplitude) of a background of gravitational waves !
[Seljak & Zaldarriaga,
1997]
(and, if present, also of rotational
modes, like in models with topological defects).
= 0. We see then that an unambiguous detection of some
level of B-type fluctuations will be a signature of the existence (and
of the amplitude) of a background of gravitational waves !
[Seljak & Zaldarriaga,
1997]
(and, if present, also of rotational
modes, like in models with topological defects).
Linear polarization is a symmetric and traceless 2x2 tensor that
requires 2 parameters to fully describe it: Q, U Stokes
parameters. These depend on the orientation of the coordinate system
on the sky. It is convenient to use Q + iU and Q -
iU as the two
independent combinations, which transform under right-handed rotation
by an angle  as (Q +
iU)' = e-2i
as (Q +
iU)' = e-2i (Q + iU) and
(Q - iU)' = e2i
(Q + iU) and
(Q - iU)' = e2i (Q -
iU). These two quantities have spin-weights
2 and -2 respectively and can be decomposed into spin ±2
spherical harmonics ±2Ylm
(Q -
iU). These two quantities have spin-weights
2 and -2 respectively and can be decomposed into spin ±2
spherical harmonics ±2Ylm
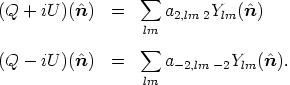
| (114) (115) |
Spin s spherical harmonics form a complete orthonormal system for
each value of s. Important property of spin-weighted basis:
there exists spin raising and lowering operators
' and
'
and
'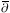 )]. By acting
twice with a spin lowering and raising operator
on (Q + iU) and (Q - iU) respectively one
obtains quantities of spin
0, which are rotationally invariant. These quantities can be
treated like the temperature and no ambiguities connected with the
orientation of coordinate system on the sky will arise. Conversely, by
acting with spin lowering and raising operators on usual harmonics
spin s harmonics can be written explicitly in terms of derivatives
of the usual spherical harmonics. Their action on
±2Ylm leads to
)]. By acting
twice with a spin lowering and raising operator
on (Q + iU) and (Q - iU) respectively one
obtains quantities of spin
0, which are rotationally invariant. These quantities can be
treated like the temperature and no ambiguities connected with the
orientation of coordinate system on the sky will arise. Conversely, by
acting with spin lowering and raising operators on usual harmonics
spin s harmonics can be written explicitly in terms of derivatives
of the usual spherical harmonics. Their action on
±2Ylm leads to
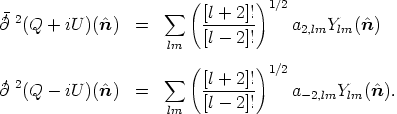
| (116) (117) |
With these definitions the expressions for the expansion coefficients of the two polarization variables become [Seljak & Zaldarriaga, 1997]
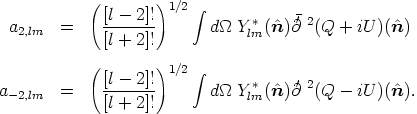
| (118) (119) |
Instead of a2,lm, a-2,lm it is convenient to introduce their linear electric and magnetic combinations

| (120) |
These two behave differently under parity transformation: while E remains unchanged B changes the sign, in analogy with electric and magnetic fields.
To characterize the statistics of the CMB perturbations only four power spectra are needed, those for X = T, E, B and the cross correlation between T and E. The cross correlation between B and E or B and T vanishes because B has the opposite parity of T and E. As usual, the spectra are defined as the rotationally invariant quantities
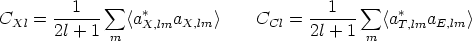
| (121) |
in terms of which on has

| (122) (123) (124) |
According to what was said above, one expects some amount of polarization to be present in all possible cosmological models. However, symmetry breaking models giving rise to topological defects differ from inflationary models in several important aspects, two of which are the relative contributions from scalar, vector and tensor modes and the coherence of the seeds sourcing the perturbation equations. In the local cosmic string case one finds that in general scalar modes are dominant, if one compares to vector and tensor modes in the usual decomposition of perturbations. The situation with global topological defects is radically different and this leads to a very distinctive signature in the polarization field.
Temperature and polarization spectra for various symmetry breaking
models were calculated by
Seljak, Pen & Turok
[1997]
and are shown in
figure 1.18. Both electric and magnetic
components of
polarization are shown for a variety of global defects. They also plot
for comparison the corresponding spectra in a typical inflationary
model, namely, the standard CDM model (h = 0.5,
 = 1,
= 1,
 baryon =
0.05) but with equal amount of scalars and
tensors perturbations (noted T / S = 1) which maximizes
the amount of B
component from inflationary models. In all the models they assumed a
standard reionization history. The most interesting feature they found
is the large magnetic mode polarization, with a typical amplitude of
~ 1 µK on degree scales [exactly those scales probed by
Hedman, et al., 2001].
For multipoles below l ~ 100 the
contributions from E and B are roughly equal. This differs
strongly
from the inflationary model predictions, where B is much smaller than
E on these scales even for the extreme case of T /
S ~ 1.
Inflationary models only generate scalar and tensor modes, while
global defects also have a significant contribution from vector
modes. As we mentioned above, scalar modes only generate E, vector
modes predominantly generate B, while for tensor modes E
and B
are comparable with B being somewhat smaller. Together this implies
that B can be significantly larger in symmetry breaking models than in
inflationary models.
baryon =
0.05) but with equal amount of scalars and
tensors perturbations (noted T / S = 1) which maximizes
the amount of B
component from inflationary models. In all the models they assumed a
standard reionization history. The most interesting feature they found
is the large magnetic mode polarization, with a typical amplitude of
~ 1 µK on degree scales [exactly those scales probed by
Hedman, et al., 2001].
For multipoles below l ~ 100 the
contributions from E and B are roughly equal. This differs
strongly
from the inflationary model predictions, where B is much smaller than
E on these scales even for the extreme case of T /
S ~ 1.
Inflationary models only generate scalar and tensor modes, while
global defects also have a significant contribution from vector
modes. As we mentioned above, scalar modes only generate E, vector
modes predominantly generate B, while for tensor modes E
and B
are comparable with B being somewhat smaller. Together this implies
that B can be significantly larger in symmetry breaking models than in
inflationary models.
String lensing and CMB polarization
Recent studies have shown that in realistic models of inflation cosmic string formation seems quite natural in a post-inflationary preheating phase [Tkachev et al., 1998, Kasuya & Kawasaki, 1998]. So, even if the gross features on CMB maps are produced by a standard (e.g., inflationary) mechanism, the presence of defects, most particularly cosmic strings, could eventually leave a distinctive signature. One such feature could be found resorting to CMB polarization: the lens effect of a string on the small scale E-type polarization of the CMB induces a significant amount of B-type polarization along the line-of-sight [Zaldarriaga & Seljak, 1998; Benabed & Bernardeau 2000]. This is an effect analogous to the Kaiser-Stebbins effect for temperature maps.
In the inflationary scenario, scalar density perturbations generate a
scalar polarization pattern, given by E -type polarization, while
tensor modes have the ability to induce both E and B types
of polarization. However, tensor modes contribute little on very small
angular scales in these models. So, if one considers, say, a standard
 CDM model, only
scalar primary
perturbations will be present without defects. But if a few strings
are left from a very early epoch, by studying the patch of the sky
where they are localized, a distinctive signature could come to light.
CDM model, only
scalar primary
perturbations will be present without defects. But if a few strings
are left from a very early epoch, by studying the patch of the sky
where they are localized, a distinctive signature could come to light.
In the small angular scale limit, in real space and in terms of the Stokes parameters Q and U one can express the E and B fields as follows
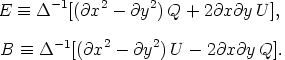
| (125) (126) |
The polarization vector is parallel transported along the geodesics.
The lens affects the polarization by displacing the apparent position
of the polarized light source. Hence, the observed Stokes parameters
 and
and
 are given in terms of the
primary (unlensed) ones by:
are given in terms of the
primary (unlensed) ones by:
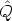 (
(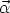 ) =
Q(
) =
Q(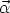 +
+
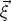 )
and
)
and
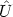 (
(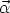 ) =
U(
) =
U(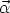 +
+
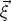 ).
The displacement
).
The displacement
 is given by the integration of the
gravitational potential along the line-of-sights.
Of course, here the `potential' acting as lens is the cosmic string
whose effect on the polarization field we want to study.
is given by the integration of the
gravitational potential along the line-of-sights.
Of course, here the `potential' acting as lens is the cosmic string
whose effect on the polarization field we want to study.
In the case of a straight string which is aligned along the y axis,
the deflection angle (or half of the deficit angle) is
4 Gµ
[Vilenkin & Shellard,
2000]
and this yields a displacement
Gµ
[Vilenkin & Shellard,
2000]
and this yields a displacement
 x =
±
x =
±
 0 with
0 with

| (127) |
with no displacement along the y axis.
 lss,s and
lss,s and
 s,us
are the cosmological angular distances
between the last scattering surface and the string, and
between the string and us, respectively. They can be computed, in an
Einstein-de Sitter universe (critical density, just dust and no
s,us
are the cosmological angular distances
between the last scattering surface and the string, and
between the string and us, respectively. They can be computed, in an
Einstein-de Sitter universe (critical density, just dust and no
 ), from
), from
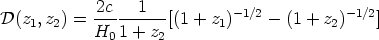
| (128) |
by taking z1 = 0 for us and z2
 1000 for the last
scattering surface; see
[Bartelmann &
Schneider, 2001].
For the usual
case in which the redshift of the string zs is well
below the
zlss one has
1000 for the last
scattering surface; see
[Bartelmann &
Schneider, 2001].
For the usual
case in which the redshift of the string zs is well
below the
zlss one has
 lss,s /
lss,s /
 lss,us
lss,us
 1 / (1 +
zs)1/2. Taking this ratio of order 1/2
(i.e., distance
from us to the last scattering surface equal to twice that from the
string to the last scattering surface) yields zs
1 / (1 +
zs)1/2. Taking this ratio of order 1/2
(i.e., distance
from us to the last scattering surface equal to twice that from the
string to the last scattering surface) yields zs
 3. Plugging in some
numbers, for typical GUT strings on has Gµ
3. Plugging in some
numbers, for typical GUT strings on has Gµ
 10-6 and so
the typical expected displacement is about less than 10 arc seconds.
Benabed & Bernardeau
[2000]
compute the
resulting B component of the polarization and find that the
effect is entirely due to the discontinuity induced by the string,
being nonzero just along the string itself. This clearly limits the
observability of the effect to extremely high resolution detectors,
possibly post-Planck ones.
10-6 and so
the typical expected displacement is about less than 10 arc seconds.
Benabed & Bernardeau
[2000]
compute the
resulting B component of the polarization and find that the
effect is entirely due to the discontinuity induced by the string,
being nonzero just along the string itself. This clearly limits the
observability of the effect to extremely high resolution detectors,
possibly post-Planck ones.
The situation for circular strings is different. As shown by
de Laix & Vachaspati
[1996]
the lens effect of such a string, when facing the
observer, is equivalent to the one of a static linear mass
distribution. Considering then a loop centered at the origin of the
coordinate system, the displacement field can be expressed very simply:
observing in a direction through the loop,
 has to
vanish, while outside of the loop the displacement decreases as
has to
vanish, while outside of the loop the displacement decreases as
 l /
l /
 , i.e.,
inversely proportional to the angle. One then has
[Benabed & Bernardeau,
2000]
, i.e.,
inversely proportional to the angle. One then has
[Benabed & Bernardeau,
2000]

| (129) |
where  l is
the loop radius.
l is
the loop radius.
This ansatz for the displacement, once plugged into the above equations, yields the B field shown in both panels of Figure 1.19. A weak lensing effect is barely distinguishable outside the string loop, while the strong lensing of those photons traveling close enough to the string is the most clear signature, specially for the high resolution simulation. One can check that the hot and cold spots along the string profile have roughly the same size as for the polarization field in the absence of the string loop. The simulations performed show a clear feature in the maps, although limited to low resolutions this can well be confused with other secondary polarization sources. It is well known that point radio sources and synchrotron emission from our galaxy may contribute to the foreground [de Zotti et al. 1999] and are polarized at a 10% level. Also lensing from large scale structure and dust could add to the problem.

| 
|
Figure 1.19. Simulations for the B field in the case of a circular loop. The angular size of the figure is 50' × 50'. The resolution is 5' (left) and 1.2' (right). The discontinuity in the B field is sharper the better the resolution. Weak lensing of CMB photons passing relatively apart from the position of the string core are apparent as faint patches outside of the string loop on the left panel. [Benabed & Bernardeau 2000]. | |
20 They actually find upper limits of 14 µK and 13µK on the amplitudes of the E and B modes, respectively, of the polarization field - more below. And, if in their analysis they assumed there are no B modes, then the limit on E improves to 10µK (all limits to 95% confidence level). Back.