3. ANALYSIS

The mathematical formulation of the decomposition of a given distribution of coplanar points, (in our case HII regions), has been given by Considére & Athanassoula (1982). We will only recall here the essential information briefly. Let (r_j, _j) be the radii and angles of the individual HII regions, and u_j = ln r_j. Their distribution can be written in terms of -functions:

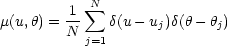
(1)

Its Fourier transform can then be written:

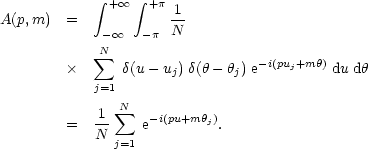
(2)

The m = 0 term corresponds to the axisymmetric component, m = 1 to the one-armed one, m = 2 to the two-armed etc. In this notation an m-armed logarithmic spiral is given by r = r₀ exp(- m / p) and its pitch angle i, by tan(i) = - m / p.

As the galaxy is projected on the sky its axisymmetric component is elliptical in shape and contributes a spurious m = 2 component around p = 0 which is added to the real m = 2 due e.g. to spiral arms or a bar. If the galaxy had been observed face-on, instead of this spurious m = 2 one would have seen an axisymmetric component. Thus a way of finding the position angle and inclination angle (hereafter PA and IA respectively) is to find the values for which the m = 0 component is maximum with respect to the other components, i.e. if we define:

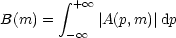
(3)

then we have to find the values of the angles that maximize the ratio

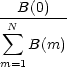
(4)

We used in this work M = 6 while omitting m = 5. A similar method has been proposed by Iye et al. (1982) not for the HII regions but for digitized images of the galaxy. The main difference is that Iye et al. take the Fourier transform of the density (r, ) while the sum in (1) gives a "mass" µ(r, ) = r² (r, ). Thus Iye et al.'s transformation will give more weight to the inner parts than ours will.