


2.3. Integral Properties of Galaxies:
The Physical Meaning of the Hubble Sequence
Classical morphology is useful because it succeeds to some extent in distinguishing galaxies which are physically different. In particular, the classification succeeds, although with considerable scatter, in ranking galaxies by values of physical parameters. The subject of this section is correlations of integral properties with stage along the Hubble sequence. By this I will mean the sequence E-S0-a-b-c-d-m-Im (i.e., the progression toward later types) (4), ignoring distinctions such as that between barred and unbarred galaxies. These most general correlations of integral properties provide important insight into galaxy formation problems.
There are two fundamental correlations implicit in the definition of Hubble types. The first is the decrease in bulge-to-disk ratio B/D along the Hubble sequence. This is illustrated in Freeman (1970, Fig. 9); Yoshizawa and Wakamatsu (1975, Fig. 2) and Boroson (1981, Fig. 9); see also Burstein (1979c); Dressler (1980b). [The parameters given in the first two papers and in Dressler (1980b) are not true bulge-to-disk ratios (section 3.4.3), but they probably order the galaxies by B/D.] All of these papers show that B/D decreases along the Hubble sequence, although the intrinsic dispersion is large (see also Sandage 1961, 1975). Thus the Hubble sequence is in part a sequence of the decreasing contribution of an ellipsoidal component which is very centrally concentrated and which formed stars early in the galaxy collapse phase. A necessary consequence is that central concentration decreases toward later types. This correlation is illustrated by photometric concentration indices (de Vaucouleurs 1974a, 1977) and by the decreasing ratio of galaxy radius to the radius at which the rotation curve peaks or levels off (Brosche 1973; Rubin, Burstein and Thonnard 1980). Both of these correlations persist over the late part of the Hubble sequence where no bulge is evident. The decrease in central concentration results in more open spiral arms at later types (Kennicutt 1981; see also Danver 1942); this is also a classification criterion.
The second fundamental correlation defining the Hubble sequence is the increasing importance of gas and young stars at later types. The Hubble sequence is observed to be one of increasingly blue color (e.g., van den Bergh 1975a, after Holmberg 1958; de Vaucouleurs 1977) and early spectral type (de Vaucouleurs 1963, after Morgan 1958, 1959). Also, the mass-to-light ratio within a Holmberg (1958) radius decreases toward later types (Faber and Gallagher 1979, Fig. 3). Of particular importance is the fact that the Hubble sequence is one of increasing H I mass fraction and H I mass-to-(optical)-light ratio (e.g., Roberts 1975; Bothun and Sullivan 1980). These correlations have led to the suggestion that the primary factor determining the Hubble stage is the amount of H I left after disk formation (e.g., Sandage, Freeman and Stokes 1970; Freeman 1975a). This is related to the fractional amount of disk, but not very closely. There are clearly many early-type galaxies which have little gas but which have structural properties similar to those of some gas-rich Sc's. The above authors give two examples of pairs of galaxies with similar structure but very different gas content and star formation. Apparently, structure and content are poorly coupled even in field galaxies.
One fundamental parameter which helps to determine Hubble types appears to be the total mass. It is now clear that the de Vaucouleurs extension beyond Sc is a sequence of decreasing mass M and luminosity L. The total mass is constant or slightly increasing between S0 and Sc, and then decreases rapidly at later types (Roberts 1975; Dickel and Rood 1978; Faber and Gallagher 1979). The observable quantity which leads to this conclusion is the maximum rotation velocity, whose dependence on type clearly resembles the above correlations (Brosche 1971). The correlation of luminosity with type has a maximum at Sbc, and decreases quite uniformly toward both earlier and later types (de Vaucouleurs 1963, 1977). (There are no dwarf Sas or Sbs, but there do exist dwarf S0s and Scs; see Strom 1980 for a possible interpretation.) Since M varies little from S0 and Sc, while L increases, the mass-to-light ratio within a Holmberg radius decreases toward later types (Faber and Gallagher's 1979 result). This decrease persists to the end of the Hubble sequence, because L decreases more slowly than M beyond Sc. The strong decrease in mass beyond Sc must contribute to the chaotic structure of very late types, because at low masses there is less differential rotation to regularize the structure. In particular, as mass decreases along the sequence Scd-Im, rotation becomes smaller compared with velocity irregularities of a few 10s of km s-1, which are produced by local effects such as stellar winds and supernovae (see Chevalier 1977; McCray and Snow 1979; Conti and McCray 1980; Silk 1980 for reviews). The details of how structure becomes chaotic as random motions become comparable to rotation have not been studied. However, it seems very likely that mass is one fundamental parameter controlling Hubble stage, although only in the range Sc-Im. The narrow subdivisions of these late stages give them undue "leverage" in correlations of integral parameters, leading to suggestions that mass controls the whole Hubble sequence (e.g., Tully, Mould and Aaronson 1982). This seems unlikely for galaxies of types S0-Sc, although the surface mass density does decrease systematically even between Sa and Sc (Rubin, Ford and Thonnard 1978b).
What is the controlling physical parameter for S0-c galaxies? Why does galaxy content correlate so poorly with optical structure? A possible answer is given in a provocative and fundamental paper by Tinsley (1981). She shows that the observed decrease of M/L within a Holmberg radius is much too small to be explained easily by models of population evolution (Figure 3). Population models which represent the observed color spread imply a variation in M/L which is up to ten times larger than that observed. A careful look at systematic effects in both the models and the data implies that the difference is significant. Only if galaxies later than ~ Sbc are all totally dominated by recent bursts of star formation can the observed M/L - (B-V) relation be modeled. This is implausible. Tinsley concludes that late-type galaxies contain proportionally more dark matter than early-type galaxies. This material is not H I; the H I masses are too small. The above result is derived with masses measured out to a Holmberg radius. Dickel and Rood (1978) and Roberts (1975) show that total M/L ratios do not decrease at all toward later types. It appears that the fraction of the total mass contributed by the halo rises even more rapidly toward later types than the fraction of the mass within a Holmberg radius.
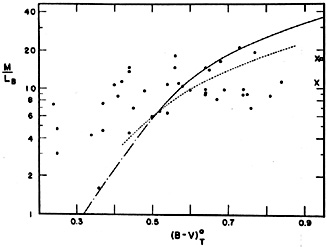 |
Figure 3. Mass-to-luminosity ratio versus color, from Tinsley (1981). The mass is calculated within the Holmberg radius; LB is the total luminosity (from Faber and Gallagher 1979, but adjusted to H0 = 100 km s-1 Mpc-1). Data for spiral galaxies are shown as dots, for S0s as crosses, and for the cores of giant ellipticals as a square. The curves are for population models in which all mass is in stars which have the initial mass function of the solar neighborhood. Different monotonically declining star formation rates (SFR) are used. The dash-dot curve is for a constant SFR with age increasing toward the right. The dotted curve is for models of age 5 × 109 yr, with a constant SFR after an initial burst which lasted 109 yr and which contained 0% of the stars at the red end of the curve and 100% at the blue end. The same models at age 1010 yr are shown by the solid curve. All of the model curves have been shifted upward by factors of ~ 6 in mass to agree with some of the data. Only if all late-type galaxies are currently undergoing bursts of star formation is the model curve (not shown) as shallow as the observed correlation. The implication is that bluer galaxies have proportionally more dark mass. |
Tinsley points out that the above result may mean that the halo mass fraction is the dominant parameter controlling Hubble types. This can potentially explain many of the observed correlations. If the visible part of a galaxy forms inside a fixed halo potential (cf. White and Rees 1978), that halo will inhibit star formation, because the gas is less self-gravitating. If star formation is reduced, inelastic collisions between clouds will have more time to form a disk. Thus, increasing the halo contribution tends to lead to a larger disk-to-bulge ratio, and also to a larger amount of residual gas after disk formation. Brosche (1973) has suggested that two parameters control Hubble types. In late-type galaxies the second parameter may be the total mass. The second parameter for S0-c galaxies is less clear. However, the initial distribution of angular momentum per unit mass of visible galaxy may be important. This, and the more fundamental ratio of visible galaxy to halo mass might explain why the Hubble sequence is one of decreasing star formation vigor and increasing dissipation during galaxy formation. As emphasized by Tinsley, this whole scenario is very speculative. Also, we need to consider possible alternatives. For example, Gunn (1981) has argued that a galaxy's position in the Hubble sequence is determined by how much gas it has accreted to form its disk. Further work is clearly needed. However, the above story is attractive because the component which contains most of the mass is the one which controls events.
At the same time, an increase of halo importance toward later types is a shocking result. The halo is the least dissipational part of a galaxy. And yet the visible part of the galaxy becomes more dissipational along the Hubble sequence. This is, there is an anticorrelation between the two least dissipational components in galaxies, halos and bulges. This emphasizes the great difference between halos and the ellipsoidal component. Discontinuities in morphology make very strong statements. Tinsley's result makes it more difficult to believe that a halo can be produced by fine-tuning any mechanism that gives a b ulge or elliptical. Exotic interpretaions of halos become more credible than they were.
4 If all S0 galaxies are most appropriately thought of as belonging to a morphological sequence parallel to the Sa-c sequence (van den Bergh 1976a), then they should not appear here. It seems likely that some S0s are formed from spirals while others are true transition objects between ellipticals and Sas. The latter are relatively more common in the field. All of the discussion in this section applies mainly to field galaxies, i.e., to objects which have been affected as little as possible by environmental processes. I therefore include S0s in the Hubble sequence. This choice actually makes little practical difference, since S0s (and also ellipticals) are largely absent from published parameter correlations.
Almost all of the discussion of this section becomes much more complicated if morphological types are commonly modified by violent events (interactions, mergers, nuclear activity, etc.) This is particularly true of galaxies in rich clusters, and, in fact, the parameter correlations with Hubble stage have large intrinsic dispersions in such clusters (e.g., Bothun 1981). Back.