3.4.3. Decomposition of Observed Profiles into Bulge and Disk Components

Figure 26 shows two galaxies in which most of the light comes from the bulge. It is clear that both galaxies have well-defined disks, but it is equally clear that the parameters of these disks cannot be determined by fitting exponentials to the observed profiles. This is the procedure used by Freeman (1970) and others; Figure 26 gives an example of how it can fail. This example is admittedly extreme. However, even when the bulge contributes less of the light, it can affect the measured disk parameters. Figure 1 of Kormendy (1977b) shows exponential and r^1/4-law fits to several S0 galaxies. Only a modest extrapolation of the r^1/4 law is needed to show that the bulge contributes light even where the disk looks exponential. Of course, this is not true in Sc-Im galaxies. In general, however, a study of disk properties requires that we decompose the observed profile into its intrinsic components (van Houten 1961; Kormendy 1977b, 1980; Burstein 1979c, d; see also de Vaucouleurs 1958, 1975; Tsikoudi 1979, 1980, and more recent papers discussed below).

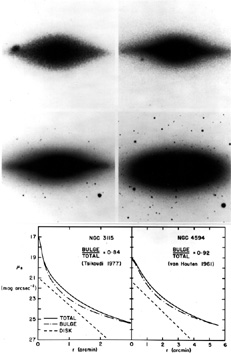Figure 26. Brightness distributions in bulge-dominated galaxies. The photographs show the edge-on S0 galaxy NGC 3115, from Kormendy (1979b). Adjacent panels in the sequence differ by a factor of two in scale. The smallest-scale panel (lower right) is 6.2 arcmin wide. The bulge is seen to dominate both at small and large radii. The bottom panels show hypothetical face-on profiles of NGC 3115 and of the similar galaxy NGC 4594, adapted from Hamabe (1982). Contrary to widespread belief, disks in bulge-dominated galaxies are best seen at intermediate and not large radii. Nevertheless, there is no radius range in which an exponential fitted to the observed profiles would give the correct disk parameters.

Techniques for decomposing brightness profiles depend on whether the galaxy is face-on or edge-on. Procedures useful for face-on galaxies have been developed by Kormendy (1977b, for one-dimensional profiles) and by Boroson (1981, for two-dimensional data). All such procedures depend on the assumption that each component is described by a fitting function. It is convenient to use r^1/4 laws for bulges and exponentials for disks. Generally the parameters derived are fairly sensitive to the adopted fitting function, but many conclusions on profile shapes are relatively model-independent (see Kormendy 1977b).

Decomposition techniques for edge-on galaxies have been developed by van der Kruit and Searle (1981a) and by Hamabe et al. (1979a, b, 1980); Hamabe (1982). The latter authors adopt a three-dimensional modified Hubble law for the bulge; van der Kruit and Searle assume that all extra light not fitted by their disk model is bulge. The disk fitting function is based on observations (section 3.4.6) of brightness profiles perpendicular to edge-on disks, which suggest:

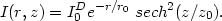(9)

Here I₀^D is a constant, and z₀ is the scale length in the z direction perpendicular to the disk. The sech² (z/z₀) dependence describes a self-gravitating sheet of stars in which is the axial velocity dispersion _z is independent of z (van der Kruit and Searle 1981a, and references therein). The adopted disk profile has a number of useful properties, discussed by van der Kruit and Searle. Neglecting internal absorption, equation (9) yields the following projections.

Face-on;

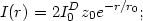(10)

Edge-on;

(11)

where K₁ is a modified Bessel function of the first kind. The edge-on case has several useful approximations.

For r >> r₀ ,

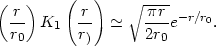(12)

That is, at large r the profile along the edge-on disk approximates the face-on exponential. Also,

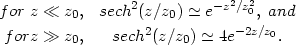(13) (14)

The observed brightness distributions are in reasonably good agreement with equations (9)-(14), and in particular, it is the observation of exponential profiles at large z perpendicular to the disk (section 3.4.6) that suggests the assumption of the isothermal sheet (see equation 14). Further details of the decomposition procedures are given in the above papers, and applications are illustrated in the following sections.

All of the above procedures have inherent strengths and weaknesses, but fortunately these are different for face-on and edge-on galaxies. In face-on galaxies, the morphology and the two-dimensional structure in the disk are clear. For example, it is possible to avoid regions of star formation and study the old disk (Schweizer 1976; Talbot et al. 1979). However, a weakness is that the results depend strongly on the extrapolation of bulge and disk fitting functions into the regions dominated by the other component. Studies of edge-on galaxies have the advantage that much of the bulge is clearly separated from the disk. The results are therefore slightly less model dependent, although the difference is not large. A second advantage is that we can study the distribution of light perpendicular to the disk. Finally, the long path length through an edge-on disk allows us to study it to very faint light levels (van der Kruit and Searle 1981a, b; 1982a). On the other hand, there are two serious disadvantages to working with edge-on galaxies. First, because of the long path length through the disk, even a small amount of internal absorption will severely affect the deduced structure and parameters. Absorption is clearly present even in some S0s (S0₂ and S0₃ galaxies, Sandage 1961), and it is very important at later Hubble types. Second, there is strong coupling between the measured disk thickness z₀ and the inclination when a galaxy is almost edge-on (Burstein 1979d). Additional problems include the fact that the azimuthal structure in the disk is integrated away by projection. In fact, even the distinction between barred and unbarred galaxies is difficult to make. Thus, decomposition techniques for face-on and edge-on galaxies have different strengths and weaknesses. They complement each other, and are both useful.

It is important to note that there are intrinsic limits to the accuracy of any profile decomposition. (1) Many disks and some bulges fail to satisfy the commonly adopted fitting functions. In any case, our experience with (exponential) bulgeless disks and (r^1/4-law) ellipticals is not necessarily a valid justification for the assumption that fitting functions extrapolate unchanged when different components can interact. At the same time, many published criticisms of profile decomposition (e.g., van der Kruit and Searle 1981b; Hamabe 1982) are unduly severe because they are based on examples which are clearly unsuitable for profile decomposition (i.e., galaxies which are dominated by either the bulge or the disk). (2) There is a continuum of transition stars between the bulge and disk (Kormendy and Illingworth 1982a). This limits in principle the accuracy of any decomposition. (3) Whenever there are more than two components present, profile decomposition is extremely difficult. This is especially true because components such as bars never occur in isolation and therefore have poorly known profile shapes. (4) Even in very suitable galaxies, there is strong coupling between bulge and disk parameters. It is therefore necessary to be very careful in applying decomposition techniques. However, it is clear that different components overlap, and therefore that such techniques are necessary.