


5.2. Bulge Components
The most obvious difference between bulges in barred and unbarred
galaxies is that many SB bulges are triaxial
(de Vaucouleurs 1974b,
1975;
Kormendy 1979a;
Sandage and Brucato
1979;
Schweizer 1980;
Kormendy 1981;
Kormendy and Koo 1982).
That is,
 50% of these bulges
appear to be elongated into secondary nuclear bars which are generally
close to perpendicular to the main bar in the disk plane. Triaxial
bulges are of interest because they may help to clarify the physics of
bars, and because they are another triaxial component which can be
involved in secular evolution.
50% of these bulges
appear to be elongated into secondary nuclear bars which are generally
close to perpendicular to the main bar in the disk plane. Triaxial
bulges are of interest because they may help to clarify the physics of
bars, and because they are another triaxial component which can be
involved in secular evolution.
Figure 40 illustrates a particularly clear example, NGC 2950 (Kormendy 1982a, Kormendy and Koo 1982). Triaxiality is implied by the fact that the bulge, bar and disk all have different position angles. Since the position angle of the disk is between those of the bulge and bar, it is not contamination by bar light which makes the position angle of the bulge different from that of the disk. Rather, the bulge must be elongated roughly at right angles to the bar in the disk plane. Since Kormendy and Koo (1982) find that these bulges are very highly flattened, I refer to them as triaxial.
Kormendy (1982a) has compared the dynamical importance of rotation in triaxial bulges, ordinary bulges, bars and elliptical galaxies. The results (Figure 46) confirm the conclusion of Kormendy and Illingworth (1982a, see section 4.2.6) that bulges of disk galaxies rotate very rapidly.
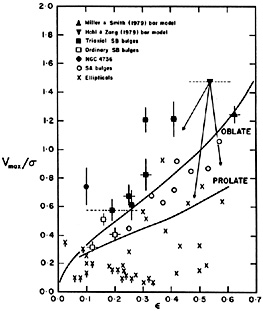 |
Figure 46. Vmax /
|
Essentially, all of the SB bulges rotate at least as rapidly as
isotropic oblate spheroids which owe their flattening to rotation. In
addition, the triaxial bulges are seen to rotate more than the ordinary
ones. The two extreme examples are NGC 3945 and 4371; these are
clearly inconsistent with the oblate line. Individually the other four
triaxial bulges are consistent with the oblate line, but on average
they have (V /
 )*
values 1.17 ± 0.04 (dispersion / 41/2)
times as large as
the prediction of the oblate models. This is significantly larger than
the average value <(V /
)*
values 1.17 ± 0.04 (dispersion / 41/2)
times as large as
the prediction of the oblate models. This is significantly larger than
the average value <(V /
 )*> = 0.90
± 0.03 for the
SA bulges. The amount
of excess rotation over the prediction of the oblate models is larger
than Figure 46 would suggest, partly because of
projection effects (see
the caption) and partly because some of the flattening is produced by
the disk potential
(Monet, Richstone and
Schechter 1981).
)*> = 0.90
± 0.03 for the
SA bulges. The amount
of excess rotation over the prediction of the oblate models is larger
than Figure 46 would suggest, partly because of
projection effects (see
the caption) and partly because some of the flattening is produced by
the disk potential
(Monet, Richstone and
Schechter 1981).
The rapid rotation of SB bulges leads to the following conclusions (Kormendy 1982a).
(1) Triaxial SB bulges resemble bars rather than elliptical galaxies. Rotation dominates the dynamics of the triaxial bulges and the n-body bar models; the latter were seen in section 5.1 to be similar to a real bar. In contrast, rotation is less important in many ellipticals.
(2) The deviation of the triaxial bulges above the oblate line is
consistent with the assumption that they are very flat. This conclusion
emerges from a consideration of projection effects for spheroids
satisfying the oblate line. If

 0.6, increasing the
inclination
moves a model downward along the oblate line. However, for
0.6, increasing the
inclination
moves a model downward along the oblate line. However, for
 > 0.7,
the oblate line becomes steeper than the projection loci. Therefore, a
highly flattened model which is viewed from outside its equatorial
plane will fall above the oblate line. For example, a disk with
Vmax ~ 200 - 300 km s-1 and
> 0.7,
the oblate line becomes steeper than the projection loci. Therefore, a
highly flattened model which is viewed from outside its equatorial
plane will fall above the oblate line. For example, a disk with
Vmax ~ 200 - 300 km s-1 and

 50 km s-1 (cf. the Galaxy) will have apparent
Vmax /
50 km s-1 (cf. the Galaxy) will have apparent
Vmax /
 values much larger than
1.0 at all inclinations of interest
here. Thus the rapid rotation of triaxial SB bulges appears to result
from a combination of bar-like dynamics and a high degree of
flattening. Not all bulge stars need to be involved: the galaxies may
just contain a highly flattened subsystem which adds to the light of a
more ordinary bulge.
values much larger than
1.0 at all inclinations of interest
here. Thus the rapid rotation of triaxial SB bulges appears to result
from a combination of bar-like dynamics and a high degree of
flattening. Not all bulge stars need to be involved: the galaxies may
just contain a highly flattened subsystem which adds to the light of a
more ordinary bulge.
Kormendy (1982a) and Kormendy and Koo (1982) suggest a possible explanation for the disk-like structure of these bulges. It is possible that "a significant fraction of the bulge in many SB galaxies consists of disk gas which has been transported to the center by the bar. As the gas accumulates it forms stars, and builds up a very centrally concentrated stellar distribution which is photometrically like a bulge but dynamically like a disk." This hypothesis is unproven but attractive, because it may tie a number of results together into a self-consistent picture.
(1) The idea is suggested by the results of calculations of the response of gas to a rotating bar (section 5.4). These calculations predict that much of the gas interior to corotation will fall to the center.
(2) A "bulge" with kinematic properties like those observed would naturally result if such gas formed stars. Support for this picture is provided by a recent observation (Pellet and Simien 1982) that the bulge of the SAab galaxy NGC 4736 also appears to rotate faster than the isotropic oblate models (Fig. 46). The disk-like nature of this bulge is also evident from its morphology (Kormendy 1980). NGC 4736 is not barred, but it is a prototypical oval and therefore also subject to the above gas transport process.
(3) Many SB bulges have smaller velocity dispersions than SA bulges of the same luminosity (Fig. 33).
(4) SB bulges are highly flattened (Kormendy and Koo 1982).
(5) Large concentrations of Population I material are seen near the centers of barred and oval galaxies. For example, many galaxies with "hot-spot nuclei" are barred or oval (Sersic and Pastoriza 1965, 1967; Sersic 1979). Often the central regions have brightness gradients as steep as those in bulges but nevertheless contain young stars (e.g., NGC 1097, Rickard 1975; NGC 3351, Morgan 1958; Vorontsov-Velyaminov, Zaitseva and Lyutyi 1972; Rubin, Ford and Peterson 1975; NGC 4314, Lynds, Furenlid and Rubin 1973; Wakamatsu and Nishida 1980; Benedict 1980).
(6) Strong nuclear activity is correlated with the presence of global asymmetry. e.g., Hummel (1981) has shown that nuclear radio continuum sources are a factor of 2 - 2.5 stronger in barred than in unbarred galaxies. Simkin, Su and Schwarz (1980) show that Seyfert galaxies are generally barred or oval (section 2.5.2). The speculation is that gas being transported to the center by a bar or oval is "feeding the monster" (Gunn 1977a) which powers the activity.
The above discussion is a good example of the application of physical morphology arguments. The evidence cited is mostly circumstantial and certainly not conclusive. However. the idea that the above observations all result in part from inward transport of gas by the bar creates a compelling amount of order in a set of apparently unconnected observations. What emerges is a specific suggestion for future work. We need to determine whether the gas transport process is quantitatively able to produce the above effects. If this is demonstrated, then the buildup of a pre-existing bulge with disk gas will be another example of a secular evolution process driven by the bar.