


4.2.2. Central Velocity Dispersions. I. The Faber-Jackson Relation
Since the measurement of rotation and dispersion profiles in
ellipticals has only recently become practical, the most extensive
stellar-kinematic measurements available are those of central velocity
dispersions  . These
allow us to estimate central mass-to-light ratios
(section 4.2.3). Also, the discovery of
a correlation between
. These
allow us to estimate central mass-to-light ratios
(section 4.2.3). Also, the discovery of
a correlation between  and metallicity
indicates that ellipticals are at least a two-parameter family
(section 4.2.4). A necessary tool for
both of these applications is a fundamental correlation between
and metallicity
indicates that ellipticals are at least a two-parameter family
(section 4.2.4). A necessary tool for
both of these applications is a fundamental correlation between
 and the total blue
luminosity LB
(Faber and Jackson
1976),
which has the approximate form
LB
and the total blue
luminosity LB
(Faber and Jackson
1976),
which has the approximate form
LB 
 n, n
n, n
 4.
4.
This relation has since been confirmed by many authors (S2BS;
Schechter and Gunn
1978;
Schechter 1980;
Terlevich et al. 1981;
Tonry and Davis 1981b;
de Vaucouleurs and
Olson 1982,
and others), who added
more measurements and refined the parameters n and the zero point.
Since LB is proportional to the adopted distance and
 is not, the
Faber-Jackson relation also provides a new way of measuring relative
distances. In particular, it has been used to map the velocity field
in the local supercluster, and thereby to derive the Local Group infall
velocity W0 toward Virgo. Two independent solutions
give the following results:
is not, the
Faber-Jackson relation also provides a new way of measuring relative
distances. In particular, it has been used to map the velocity field
in the local supercluster, and thereby to derive the Local Group infall
velocity W0 toward Virgo. Two independent solutions
give the following results:
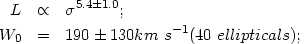 |
(20) |
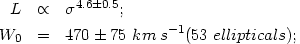 |
The power n of the Faber-Jackson relation is not sensitive to the Virgocentric flow field. Kormendy and Illingworth (1982b) obtain n = 5.4 (+0.9, -0.7) by assuming a uniform Hubble flow and n = 5.2 (+0.8, -0.6) based on a linear model (Schechter 1980) with W0 = 300 km s-1 (Aaronson et al. 1982). I will adopt n = 5.4 here, but note that this is uncertain, with values as small as n = 3.6 ± 0.3 reported (de Vaucouleurs and Olson 1982). The adopted relation is shown in Figure 33.
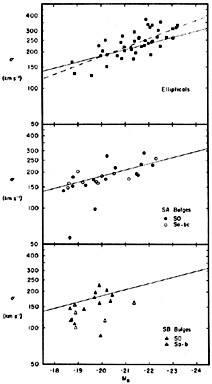 |
Figure 33. Correlations between central
velocity dispersions |
Recent work suggests that the Faber-Jackson relation may not be a
simple power law. At the low-luminosity end, a downward curvature of
the relation in Figure 33 is indicated by
Tonry's (1981)
analysis of galaxies down to MB = -18.0. This study
has the advantage that the
galaxies are all in the Virgo cluster, so relative distance errors
cannot affect the value of n. For ellipticals fainter than
MB ~ - 20, Tonry finds that
LB 
 3.2±0.2.
Similarly,
Davies et al. (1983)
find n = 2.4 ± 0.9 for 14 ellipticals fainter than
MB = -20, and
n = 4.2 ± 0.9 for 30 brighter ellipticals. If this effect is
confirmed
in larger samples, several explanations are possible. (1) The mass-to-light
ratio may be a steeper function of luminosity in faint galaxies
than in bright ones; see section 4.2.3.
(2) Rotation may provide some of the
dynamical support in low-luminosity ellipticals, which are known to
rotate rapidly (section 4.2.6). (3)
Velocity dispersion gradients may be
averaged by the large measuring aperture used,
3" × 12". This is a
special problem for faint ellipticals because they, have small dynamical
characteristic radii. If the
3.2±0.2.
Similarly,
Davies et al. (1983)
find n = 2.4 ± 0.9 for 14 ellipticals fainter than
MB = -20, and
n = 4.2 ± 0.9 for 30 brighter ellipticals. If this effect is
confirmed
in larger samples, several explanations are possible. (1) The mass-to-light
ratio may be a steeper function of luminosity in faint galaxies
than in bright ones; see section 4.2.3.
(2) Rotation may provide some of the
dynamical support in low-luminosity ellipticals, which are known to
rotate rapidly (section 4.2.6). (3)
Velocity dispersion gradients may be
averaged by the large measuring aperture used,
3" × 12". This is a
special problem for faint ellipticals because they, have small dynamical
characteristic radii. If the
 - rc
relation of Figure 22 holds for these galaxies, they have core radii
rc ~ 0.5". Any dispersion
gradients generally begin just outside r = rc (see
Fig. 35). But
rc is much smaller than the measuring aperture.
- rc
relation of Figure 22 holds for these galaxies, they have core radii
rc ~ 0.5". Any dispersion
gradients generally begin just outside r = rc (see
Fig. 35). But
rc is much smaller than the measuring aperture.
At the high-luminosity end, Malumuth and Kirshner
(1981,
Fig. 1) suggest that the
log -
MB correlation levels off, in that brightest
cluster galaxies do not have larger dispersions than slightly fainter
galaxies. The deviation from the adopted
L
-
MB correlation levels off, in that brightest
cluster galaxies do not have larger dispersions than slightly fainter
galaxies. The deviation from the adopted
L 
 n
relation is especially
large for three cD galaxies measured. However, most of this effect is
due to the contribution to MB of the cD halo; when
this is removed
the galaxies do not deviate significantly. As noted by Malumuth and
Kirshner, this is consistent with the assumption (see
section 3.3.4)
that the halos are dynamically distinct features added to basically normal,
although very bright, ellipticals.
n
relation is especially
large for three cD galaxies measured. However, most of this effect is
due to the contribution to MB of the cD halo; when
this is removed
the galaxies do not deviate significantly. As noted by Malumuth and
Kirshner, this is consistent with the assumption (see
section 3.3.4)
that the halos are dynamically distinct features added to basically normal,
although very bright, ellipticals.
| E (n = 5.4): |  21 = 21 = |
217 ± 6 km s-1 | E (n=7.8): |  21 = 21 = |
222 ± 6 km s-1 |
| SA0 : | 218 ± 10 km s-1 | SA0 : | 211 ± 9 km s-1 | ||
| SAa-bc : | 217 ± 9 km s-1 | SAa-bc : | 205 ± 7 km s-1 | ||
| SB0-b : | 185 ± 10 km s-1 | SB0-b : | 172 ± 10 km s-1 |
In section 3.4.1 I discussed a number of physical differences between ellipticals and the bulges of spiral galaxies. The Faber-Jackson relation provides another probe of such differences. Interestingly, the nuclear dynamics of ellipticals and normal bulges are found to be indistinguishable.
Early reports seemed to tell a different story.
Whitmore, Kirshner and
Schechter (1979)
and Whitmore and Kirshner
(1981,
hereafter collectively WKS) found that ellipticals and S0s have the same
L 
 n relation,
but bulges of spiral galaxies have velocity dispersions smaller by
17 ± 8% than ellipticals of the same luminosity. If
we use as the zero point of the
L
n relation,
but bulges of spiral galaxies have velocity dispersions smaller by
17 ± 8% than ellipticals of the same luminosity. If
we use as the zero point of the
L 
 n relation the
dispersion
n relation the
dispersion  21 at
MB = - 21(H0 = 50 km s-1
Mpc-1), then WKS found
21 at
MB = - 21(H0 = 50 km s-1
Mpc-1), then WKS found
 21 = 228
± 11 km s-1 in ellipticals,
220 ± 15 km s-1 in S0 bulges and 190 ± 10
km s-1 in
spiral bulges. All bulge magnitudes were corrected for disk light as
in section 3.4.3. Several effects could
contribute to the above difference.
(1) Much of the photometry used was not accurate enough for reliable
profile decomposition. (2) Rotation of bulges would decrease the
amount of velocity dispersion required to support the galaxy. However,
S0 bulges rotate as rapidly as those of spirals
(section 4.2.6) and are not
colder than ellipticals. (3) The bulges could have lower M/L values
due to recent star formation. In fact,
Whitmore and Kirshner
(1981)
make the prophetic statement that "most of the spiral bulges do fall
very close to the [L
21 = 228
± 11 km s-1 in ellipticals,
220 ± 15 km s-1 in S0 bulges and 190 ± 10
km s-1 in
spiral bulges. All bulge magnitudes were corrected for disk light as
in section 3.4.3. Several effects could
contribute to the above difference.
(1) Much of the photometry used was not accurate enough for reliable
profile decomposition. (2) Rotation of bulges would decrease the
amount of velocity dispersion required to support the galaxy. However,
S0 bulges rotate as rapidly as those of spirals
(section 4.2.6) and are not
colder than ellipticals. (3) The bulges could have lower M/L values
due to recent star formation. In fact,
Whitmore and Kirshner
(1981)
make the prophetic statement that "most of the spiral bulges do fall
very close to the [L

 n] line for
ellipticals, and only a few
galaxies (perhaps NGC 4303 and NGC 4321 . . . ) undergoing a recent burst
[of star formation] provide the increased scatter and the gap with the
ellipticals."
n] line for
ellipticals, and only a few
galaxies (perhaps NGC 4303 and NGC 4321 . . . ) undergoing a recent burst
[of star formation] provide the increased scatter and the gap with the
ellipticals."
Recently,
Kormendy and
Illingworth (1982b)
have re-examined the
L 
 n relation
for disk-galaxy bulges, motivated by the following
worries about the WKS analysis. First, many WKS "bulges" clearly
contain Population I material. Essentially, the galaxies are too late in
type to contain bulges which resemble ellipticals. What is the
L
n relation
for disk-galaxy bulges, motivated by the following
worries about the WKS analysis. First, many WKS "bulges" clearly
contain Population I material. Essentially, the galaxies are too late in
type to contain bulges which resemble ellipticals. What is the
L 
 n
relation for bulges, like those of M31 and M81, which are similar to
ellipticals? Second, we will see in
section 5 that bulges of barred galaxies
are more disk-like than SA bulges. Do they also have different
L
n
relation for bulges, like those of M31 and M81, which are similar to
ellipticals? Second, we will see in
section 5 that bulges of barred galaxies
are more disk-like than SA bulges. Do they also have different
L 
 n
relations? Third, Kormendy and Illingworth retain only those galaxies
with photometrically well determined bulge magnitudes. Finally, they
verify that plausible Virgocentric flow fields do not affect the
conclusions.
n
relations? Third, Kormendy and Illingworth retain only those galaxies
with photometrically well determined bulge magnitudes. Finally, they
verify that plausible Virgocentric flow fields do not affect the
conclusions.
The results are shown in Figure 33. Galaxies which clearly have young stars in their nuclei are omitted (e.g., NGC 4321, see the spectrophotometry of Turnrose 1976). There is then no difference in the slope or zero point for ellipticals, or bulges of unbarred S0 or Sa-bc galaxies. On the other hand, many bulges of barred galaxies, even SB0s, have lower dispersions than SA bulges of the same luminosity. A possible interpretation is discussed in section 5.2.
Evidently the difference in zero point found by WKS was due to the inclusion of late-type galaxies whose disks contribute light even at the center, and barred galaxies whose bulges differ systematically from SA bulges. The global differences between ellipticals and ordinary bulges are not reflected in their central dynamics, to the accuracy of the present observations. This is not implausible if the global differences are caused by a combination of rotation and the disk potential in bulges; neither effect should be very important near the center.