


4.1. Photoionization equilibrium
Consider an isolated cloud exposed to a monodirectional flux of ionizing
photons.
Let L be the
monochromatic luminosity of the central source, per unit
frequency, and r the cloud-center distance. Consider a point at a
depth s into
the cloud, where the optical depth is
be the
monochromatic luminosity of the central source, per unit
frequency, and r the cloud-center distance. Consider a point at a
depth s into
the cloud, where the optical depth is

 . Assume also that all ions
are in their ground level and the ionization field is not very
intense. The rate of photoionization
events per unit volume, of an ion Xi with a number
density NXi, is
. Assume also that all ions
are in their ground level and the ionization field is not very
intense. The rate of photoionization
events per unit volume, of an ion Xi with a number
density NXi, is
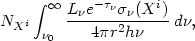
| (2) |
where  0 is the
threshold ionization frequency and
0 is the
threshold ionization frequency and

 (Xi) the
photoionization
cross section. The rate of the inverse process, radiative recombination, is
(Xi) the
photoionization
cross section. The rate of the inverse process, radiative recombination, is
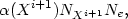
| (3) |
where Ne is the electron density and
 (Xi+1)
is a recombination coefficient which includes recombinations to all levels.
(Xi+1)
is a recombination coefficient which includes recombinations to all levels.
If L , is not
varying in time or the recombination time, trec = 1 /
, is not
varying in time or the recombination time, trec = 1 /
 (Xi+l)
Ne,
is short enough, the ionization fraction
NXi+1 / NXi
can be solved for by equating
(2) and (3). The overall degree of ionization is found by solving such
equations
for all successive stages of ionizations, with the additional requirement on
the total abundance of X,
(Xi+l)
Ne,
is short enough, the ionization fraction
NXi+1 / NXi
can be solved for by equating
(2) and (3). The overall degree of ionization is found by solving such
equations
for all successive stages of ionizations, with the additional requirement on
the total abundance of X,
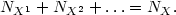
| (4) |
Evidently, the degree of ionization depends on the ratio of the ionizing photon flux to the gas density. It is convenient therefore to introduce an ionization parameter that specifies this ratio. The ionization parameter for hydrogen, at the illuminated face of the cloud, is designated U and is given by
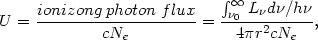
| (5) |
where c is the speed of light which is introduced to make U dimensionless. (1) As explained below, typical values for U in AGN clouds are 10-3-1.
In principle there is a different ionization parameter for each element and at each point in the cloud. In practice, U as defined for hydrogen at the front of the cloud, is very useful and characterizes the overall level of ionization very well. For example, in quasars' BLR clouds,
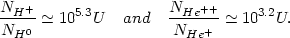
| (6) |
This approximate relation is already enough to estimate the size of the
broad line clouds. The photoionization cross section for hydrogen
(
 (H0)) at
1 Rydberg is about 6.3 × 10-18
cm2. Using the estimated degree of ionization
from (6) with U = 0.1, for a density of Ne =
NH = 1010 cm-3, we find
that an optical depth of 10 at the Lyman limit corresponds to a physical
thickness of
ionized hydrogen of about 3 × 1012 cm. The column
density of ionized gas is
about 3 × 1022 cm-2. The amount of
neutral material is not well known (see
below) but a rough estimate for its column density is some 10 times the
column
of ionized gas. If clouds are roughly spherical, and they cover about
10% of the
source (chapter 2), we need more than 107 clouds in a bright
AGN whose BLR
radius is of the order of 0.1 pc. (chapter 8). The associated filling
factor (the
fraction of the total volume filled with such clouds) is tiny, of the
order of
10-12! The number of clouds is smaller for less luminous
AGNs, especially if
they are non-spherical, or have much larger neutral zones. Note also the
small
Compton depth of such clouds, which is the main reason for neglecting
electron scattering in most of the following discussion.
(H0)) at
1 Rydberg is about 6.3 × 10-18
cm2. Using the estimated degree of ionization
from (6) with U = 0.1, for a density of Ne =
NH = 1010 cm-3, we find
that an optical depth of 10 at the Lyman limit corresponds to a physical
thickness of
ionized hydrogen of about 3 × 1012 cm. The column
density of ionized gas is
about 3 × 1022 cm-2. The amount of
neutral material is not well known (see
below) but a rough estimate for its column density is some 10 times the
column
of ionized gas. If clouds are roughly spherical, and they cover about
10% of the
source (chapter 2), we need more than 107 clouds in a bright
AGN whose BLR
radius is of the order of 0.1 pc. (chapter 8). The associated filling
factor (the
fraction of the total volume filled with such clouds) is tiny, of the
order of
10-12! The number of clouds is smaller for less luminous
AGNs, especially if
they are non-spherical, or have much larger neutral zones. Note also the
small
Compton depth of such clouds, which is the main reason for neglecting
electron scattering in most of the following discussion.
The ionization parameter is also a measure of the way the ionization structure is changing, and it is easy to show that the thickness of ionization fronts is inversely proportional to U. Thus a large ionization parameter corresponds to sharp transition between successive stages of ionization and small U results in thick regions of gradual change in the level of ionization.
The steady state ionization structure is obtained by solving the ionization and recombination equations for all elements and at all points in the cloud. Ionization from all levels must be considered as well as corrections due to induced processes. For example, the photoionization rate per unit volume from the hydrogen level i is
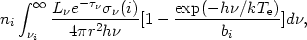
| (7) |
where the second term on the right is the correction due to induced recombination and bi is the departure coefficient for the level. The continuum optical depth includes a similar correction factor, thus
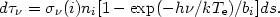
| (8) |
Stimulated processes are important in regions of intense radiation fields and they are usually more important for high energy levels. The innermost part of the BLR is one place where they should not be neglected.
The photoionization of heavy ions by high energy X-ray photons is somewhat more complicated to treat. Such photons can eject a K-shell electron and the following ionic readjustment can often cause a removal of an additional electron. This "Auger effect" couples the ion Xi to Xi+2. The process is important in regions of the cloud where much of the softer ionizing radiation has already been exhausted and only the small cross-section, high energy photons can penetrate. The removal of L-shell electrons (2s, 2p) is important too at high photon energies. Generally speaking, in a solar composition material with Te ~ 104 K, the main sources of opacity between 1 and 20 Ryd are H0, He0 and He+1. The metal opacity is more important at higher energies; carbon, nitrogen and oxygen up to ~ 50 Ryd and iron etc. beyond that. Much of the X-ray opacity is due to K-shell absorption, which is not very sensitive to the exact degree of ionization. Thus the opacity at those frequencies reflects mainly the chemical composition of the gas and not its degree of ionization.
Photoionization from excited levels is, in some cases, of great importance. An example is the ionization of O++ from the two metastable levels, 1S0 and 1D2. These levels are in their Boltzmann population in AGN high density clouds, and photoionization out of them has a comparable rate to the ground level photoionization. The ground level ionization threshold of O++ is just short of the He+ ionization edge, at 54.4 eV. The gas opacity at all energies higher than 54.4 eV is almost entirely controlled by He+, whose abundance is very high, and the O++ ground level opacity plays almost no role. The O++ metastable levels ionization is about 5 eV lower than the ground level ionization. This extends the O++ photoionization cross section into frequencies where it may become a dominant source of opacity. It can influence, in some cases, the ionization of C++ (threshold at 47.9 eV) which has a large effect on the local cooling and line emission. Other important examples of this type are ionization from excited states of N0 and Mg+.
The ionization structure in AGN clouds is very different from that of HII regions and planetary nebulae. The clouds can be thick enough to be highly ionized (N+4, O+5) at their illuminated face and almost completely neutral at the back. The large flux of X-ray photons maintains a low degree of ionization (~ 10%) over a large part of the cloud, more than 90% of its thickness in some cases. Such extended low ionization regions are thought to be the origin of the strong FeII and MgII lines. The ionization structure in the highly ionized part depends on the value of U. Large (~ 0.1 - 1) U results in sharply defined ionization fronts. Smaller U enables several stages of ionization to co-exist over large parts of the cloud.
1 The term ionization parameter
has been used loosely in the literature. In some papers it
is not divided by c, which leave it in velocity units. Some
authors define it as
L /
4
/
4  r2
hNe
at a chosen frequency (usually at 1 Ryd.) and in other cases (chapter 9)
it is the ratio of
radiation pressure to gas pressure (i.e. divided by the temperature).
Back.
r2
hNe
at a chosen frequency (usually at 1 Ryd.) and in other cases (chapter 9)
it is the ratio of
radiation pressure to gas pressure (i.e. divided by the temperature).
Back.