4.2. Thermal Equilibrium

The equilibrium temperature of the gas is the result of heating, by absorption of the central source radiation, and cooling via several atomic processes. The temperature referred to is the kinetic temperature of the charged particles, or the electron temperature, T_e, which is well defined for all particles with a Maxwellian distribution of kinetic energies. It should not be confused with the radiation temperature (or color temperature), T_rad, characterizing the radiation field or the excitation temperature, T_ex, describing the populations of the atomic levels. Conditions in gaseous nebulae are far from thermodynamic equilibrium and T_e is usually different from both T_rad and T_ex. However, in some AGN clouds the density and optical depth are large enough so that for some ions T_ez = T_ex, i.e. the level populations are given by the Boltzmann excitation equation.

The most important heating-cooling processes in AGNs clouds are:

4.2.1. Bound-free heating-cooling. Consider the absorption of a photon with energy h by the ion Xⁱ in a level whose threshold ionization frequency is ₀. The initial kinetic energy of the freed electron is (h - h₀), and this energy is quickly spread, by elastic collisions, among the charged particles. ⁽²⁾ The heating rate per unit volume due to this ionization is

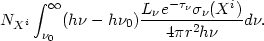
(9)

Summation over all levels of all elements gives the total bound-free heating. A correction due to stimulated recombination, as in equation (7), must be included in some cases.

The average energy of a recombining electron is close to kT_e and the total energy loss due to spontaneous radiative recombination is obtained by summing over expressions of the form

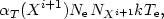
(10)

for all ions and all levels. Here _T is an energy averaged recombination coefficient which is somewhat different from the coefficient used in equation (3).

4.2.2. Free-free heating-cooling. The free-free heating rate per unit volume, due to the ion X^+Z, is

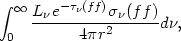
(11)

where

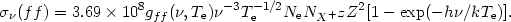
(12)

In this equation g_ff(, T_e) is the thermal average of the Gaunt factor and allowance is made for stimulated emission.

Free-free absorption is a significant heating source for the gas in cases of intense low frequency radiation and large columns of ionized gas. Most low density nebulae are optically thin to free-free absorption, but some BLR clouds, with densities exceeding 10¹⁰ cm^-3 and large column densities, may become opaque to this radiation, especially at low frequencies. For example, a unit free-free optical depth at a wavelength of 30 µm, for N_e = 10¹⁰ cm^-3 and T_e = 10⁴K, is obtained for a column density of 10²² cm^-2.

Free-free cooling is the result of bremsstrahlung events converting some kinetic energy into radiation via electron-ion Coulomb collisions. The rate, per unit volume, is given to a good approximation by

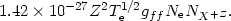
(13)

The large abundance of hydrogen and helium ensures that their contribution to free-free cooling is the most important one.

A modification of the heating-cooling rate is required in cases of significant free-free optical depth, since some of the radiation is re-absorbed and heating by the diffuse free-free radiation was not included. An approximate way to introduce the correction is to multiply the cooling rate by the factor exp(-h _cut / kT_e), where _cut is the depth dependent frequency, where the gas becomes optically thin to free-free absorption.

4.2.3. Collisional excitation and de-excitation heating-cooling. Inelastic collisions of free electrons with ions, followed by a radiative decay, convert kinetic energy into excitation energy and contribute to the cooling of the gas. Collisional de-excitation returns energy to the electron gas and is thus a heating process. It is convenient to discuss the net cooling, which is the cooling minus heating, per unit volume and time.

Consider the two level system, i and j (j > i), with statistical weights g_i and g_j respectively. The levels are coupled by an optically thin line, of energy E_ij and a radiative transition rate A_ji. The collisional excitation rate between the levels is

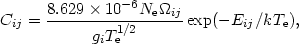
(14)

and the collisional de-excitation rate

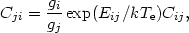
(15)

where _ij is the effective, temperature averaged, collision strength. In the absence of other populating mechanisms, the relative population of the levels is

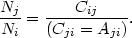
(16)

A useful concept is the so called "critical density", which is obtained for each transition by solving for the electron density for which C_ji = A_ji. Collisional de-excitation can be neglected for densities much smaller than this critical density, while the Boltzmann excitation equation can replace (16) for densities much above it.

The net cooling is the energy emitted by the atoms per unit volume and time

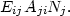
(17)

In the limit of low density this is reduced to

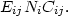
(18)

Thus, in this limit, the net cooling is proportional to N_e². In the high density limit N_j N_i and the net cooling is proportional to the gas density. Since the net cooling is basically the line emission, this is also the density dependence of the emergent line flux.

The formalism used here is easily generalized to a multi-level system and to the case where other atomic processes contribute to the level populations.

The steady state electron temperature is obtained by solving the simple energy conservation equation

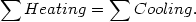
(19)

This requires the full solution of the statistical equilibrium equations at all points in the cloud. The ionization and thermal solutions are of course coupled and iterative methods must be used to solve them, simultaneously.

² see however the note below about secondary electrons. Back.