10.5. AGN Accretion Disks

10.5.1 Theoretical disk models. Theoretical justifications for accretion disks and their properties are discussed by R. Blandford. Here we limit the discussion to the observational implications of geometrically thin, optically thick, accretion disks.

The calculations of the radiation emitted by thin accretion disks, around massive black holes, are extremely complex. There were several attempts to calculate the spectrum of "bare disks", i.e. those without a corona, but none combined a full atmospheric solution with a general relativistic treatment. The most sophisticated calculations, so far, combine a full relativistic treatment with a simplified transfer solution (all examples in this chapter are from this set of calculations). Differences between existing models are large, reflecting, most probably, the different approximation used.

The following is a short summary of those results that are most relevant to the observations of AGNs.

a: The spectrum of "bare disks" with L/L_Edd ~ 0.1, gives a fair fit to the observations of many AGNs, in the spectral range 1000-6000Å. Disks around fast rotating black holes are hotter, and give a somewhat better fit to the observed spectra. The largest accretion rate allowed by the models, expressed in units of L/L_Edd, is about 0.3. For larger accretion rate, the geometrical thickness of the disk is too large to be consistent with the "standard thin disk" assumption. The disks are radiation pressure dominated and their self-gravity radius is relatively small.

b: The polarization of AGN disks is considerably smaller than the polarization of Newtonian disks, with fully scattering atmospheres.

c: The soft X-ray continuum (0.3-2 keV) of many AGNs is too strong to be fitted by the disk models that fit the observed optical-ultraviolet continuum. The hard (2-20 keV) X-ray continuum of all AGNs is inconsistent with standard thin disk spectra.

d: Aspect dependent effects are very important. A simple, wavelength independent limb darkening law of the form

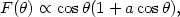
(102)

with a ~ 1.5, gives a good approximation to the angle dependent flux at optical wavelengths. This limb darkening law fails at very short wavelengths, where relativistic effects dominate the emission. In particular, the continuum of an edge-on disk is much harder than that of a face-on disk. This is illustrated in Fig. 32 that shows the flux emitted by the disk at three inclination angles. The relativistic effects are important at soft X-ray energies for low luminosity AGNs, and at ultraviolet energies for high luminosity (i.e. more massive central black hole) objects.

e: The lack of a direct observational method to find the inclination angle in individual objects, implies that the fitting of AGN continua by disk models is not unique. It can amount to a factor of 10 uncertainty in the inferred central mass and accretion rate for a given object.

Figure 32. Theoretical thin disk spectra at three different viewing angles. The infrared and the X-ray continua are approximated by power-laws, with spectral indices of 1.4 and 0.7, respectively (courtesy of A. Laor).

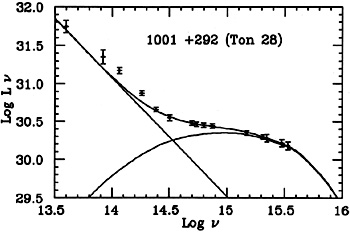
A fit of a theoretical disk model to the observation of a particular quasar is shown in Fig. 33. There are three major continuum components in this fit. The first is an infrared power-law, made to fit the 1-3µm range, and extended into shorter wavelengths with the same slope. Such a component is always needed since the disk emission cannot explain the observed infrared continuum. The assumption of a power-law shape is neither certain nor essential. It is a reasonable guess over the limited wavelength range in question, but other possibilities, such as thermal emission by dust and stars, can be made to fit the data, at least in some cases. The second component is the thermal disk emission, It is about as intense as the infrared component at lµ and produces most of the emission at shorter wavelengths. There are indications that the relative contribution of this component, compared with the infrared component, is larger in more luminous objects. Finally a third, X-ray component, is needed in all cases. It dominates the emission at energies larger than about 1 keV, the energy where all disk models are found to radiate well below the observed flux. It is important to note that despite the very good match to the observed spectrum, in this and other cases, some AGN spectra cannot be fitted by any disk model calculated so far.

Figure 33. A model fit to the spectrum of the quasar Ton 28, showing the infrared power-law component and a theoretical disk continuum (courtesy of A. Laor).

10.5.2 Thin accretion disks and the Baldwin relationship. The successful fitting of observed AGN continua by disk models does not give a conclusive evidence for the presence of such disks. There are other continuum emission processes that are consistent with the data and the model uncertainties are large. There are other ways to search for such disks, using viewing angle related effects. The observed disk flux depends on the inclination to the line of sight. On the other hand, the emission line flux originates, presumably, in isotropically emitting clouds, and is independent on the observer's viewing angle. Thus the line-to-continuum ratio, i.e. the line EW, is a measure of the disk inclination.

The intrinsic line/continuum ratio can differ from object to object and it is not possible to determine the disk inclination by a single EW measurement. The statistical properties of a large sample are more promising in this respect. The disk continuum flux is roughly proportional to cos (102) and the line EW, assuming isotropic line emission is, therefore, proportional to 1 / cos . The probability distribution of equivalent widths, in a sample with random disk orientations, is thus

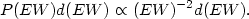
(103)

The observed EW distributions in several AGN samples is consistent with that.

Testing the EW distribution, and other disk-related phenomena, is hampered by various selection effects. Some of those are well known and are related to the discovery methods and the incompleteness of magnitude limited samples. Thin disks, if they exist, may introduce yet another selection effect. Such objects are brighter when observed face-on, which may cause the drop-out of edge-on objects from flux limited samples. The effect is most difficult to estimate in objective-prism surveys, where the objects are detected due to some combination of their continuum brightness and line strength. Searching for thin disks in big AGN samples, by ways of their characteristic EW distribution, can only be performed if the discovery technique is independent of the disk properties. Radio selected samples, especially those found by their extended, steep radio spectrum, may prove to be most appropriate for that.

An example illustrating all this is shown below. Several theoretical thin disk models, with 10⁸ M 10¹⁰ M, 0.1 cos() 1 and two values of L/L_Edd, 0.1 and 0.3, were calculated to produce a set of theoretical continua. These were used in photoionization calculations to find theoretical L intensities, like in chapter 4. The resulting theoretical I(L) vs. L(1215Å) correlation is shown in Fig. 34. The horizontal lines in the diagram are due to the fact that a given L flux is associated with a range of continuum fluxes, because of the disk inclination.

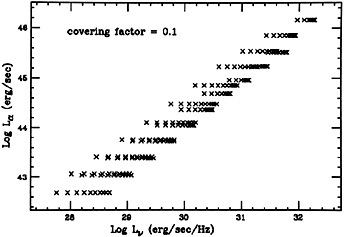
Figure 34. Theoretical L vs. L(1215Å) for disk continua.

The same data, transformed into an EW(L) vs. L₁₂₁₅ by assuming a constant covering factor of 0.1, is shown in Fig. 35. The previous horizontal lines are transformed into diagonal lines and there is a tendency for EW(L) to decrease with increasing L₁₂₁₅. This is due to the combined effect of the disk inclination and the disk ionizing flux being softer in more luminous (larger mass) systems.

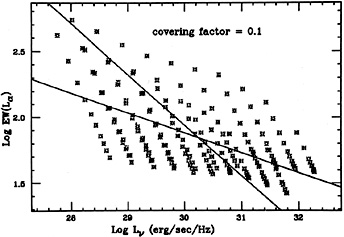
Figure 35. Theoretical EW(L) vs. L(1215Å) for AGN disks.

The theoretical distributions in Figs. 34 and 35 are similar to the observed distributions in Figs. 28 and 31, and can explain, therefore, the Baldwin relationship. They are also consistent with the observational finding that the slope of the Baldwin relation depends on the luminosity range of the sample. In this case, there is no need to assume a luminosity dependence of the covering factor or the ionization parameter. Note again the possible selection effects and the inhomogeneity of the sample used here.