The main task of Observational Cosmology is to identify which of the idealized models, that theoretical Cosmologists construct, relates to the Universe we live in. One may think that since we cannot perform experiments and study, in a laboratory sense, the Universe as a whole, this is a futile task. Nature however has been graceful, and through the detailed and exhaustive analysis of the detected electromagnetic radiation emitted from the different photon-generating processes, we can do wonders!
Among the many important tasks of Observational Cosmology is the determination of the total mass-energy density of the Universe, the rate of its expansion, its age, the amount of ordinary and exotic matter that it contains, as well as to quantify in a objective and bias free manner the large-scale distribution of matter, as traced by galaxies, clusters of galaxies and AGN's for example.
However, these tasks are not easy to fulfil. Subjective (instrumentation, available funds, technological limitations etc) as well as objective (observational biases, limitations due to our position in space-time, etc) difficulties exist. Furthermore, we do not know whether the Universe accessible to our observations is representative of the whole Universe. A positive answer to this question is essential in order to meaningfully compare observations with theory. Under the assumption that the Universe is homogeneous and isotropic (in a statistical sense), well separated regions can be viewed as independent realizations of the same formation process. Therefore many of such regions constitute an ensemble and thus we can employ statistical techniques in our study.
In the classical Big-Bang cosmological framework the Universe indeed is considered homogeneous and isotropic on the large-scales. The most general metric satisfying this assumption, the so-called Cosmological Principle, is the Robertson-Walker metric (cf. [183], [35]), [112]):
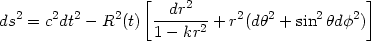
| (1) |
where R(t) is the expansion factor, k is a
constant, related to curvature of space and (r,
,
) are spherical-polar
coordinates. The main observational evidence that supports the choice of
this model is:
d.
However, the observed matter distribution in the Universe is very inhomogeneous on small-scales. So, what evidence do we have supporting the validity of the Cosmological Principle?
Firstly, the Hubble’s law is directly obtained if one assumes a
homogeneous expansion of the Universe, ie., if a length
is expanded by
a factor R(t), then after some time we have d =
R(t) .
Differentiating we obtain the Hubble law:
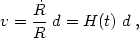
| (2) |
where H(t), at the present time (t = 0), is the Hubble constant. Secondly, observations of distant extragalactic radio sources have shown that they are distributed across the sky in a uniform way. Other supporting evidence is provided from the decreasing - with scale - correlations of extragalactic objects and the directional independence of the correlation function. However, the most remarkable confirmation that the Universe is homogeneous and isotropic and also that it evolved from a hot dense past, was the discovery of the cosmic microwave background radiation and its high degree of isotropy across the sky. This radiation has been interpreted as the relic radiation from the time that matter decoupled from radiation, which has been freely travelling ever since. The high degree of isotropy of the CMB is direct evidence that the Universe was highly isotropic at the epoch of decoupling (z ~ 1100) to one part in 105 on scales from arc-minutes to 90°, once we subtract a local dipole anisotropy, attributed to our peculiar motion with respect to the rest-frame defined by the CMB.