


1.1. Basic Elements of Dynamical Cosmology
Out of the many
parameters which are essential for accurately determining the global
dynamics and the formation history of the Universe; three clearly stand
out: the Hubble constant, H0, which tells us the
expansion rate of the Universe, the matter density parameter,
 m, which
tells us how much
matter, being baryonic or exotic, the Universe contains and the
Cosmological constant,
m, which
tells us how much
matter, being baryonic or exotic, the Universe contains and the
Cosmological constant,
 , which tells us
whether the universe is filled
with an extra repulsive force. The way in which these parameters affect
the cosmological evolution, are determined by the gravitational field
equations and the assumed equation of state. Below, I will sketch the
basic framework of standard Cosmology, in order to derive the
interrelations of these parameters and how they relate to the global
dynamics of the Universe.
, which tells us
whether the universe is filled
with an extra repulsive force. The way in which these parameters affect
the cosmological evolution, are determined by the gravitational field
equations and the assumed equation of state. Below, I will sketch the
basic framework of standard Cosmology, in order to derive the
interrelations of these parameters and how they relate to the global
dynamics of the Universe.
Friedmann Equations: Within the context of a homogeneous and isotropic Universe we can derive the cosmological evolution equations using either Einstein's field equations or Newtonian gravity. The latter is possible exactly because of the Cosmological Principle, ie., we can consider any volume element, as small as necessary for Newtonian gravity to apply, as being representative of the Universe as a whole. We will derive the evolution equations for the Newtonian case, using however as an active mass density:
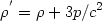
| (3) |
which is given within the framework of general relativity for a
homogeneous and isotropic fluid with density
 and pressure
p.
and pressure
p.
In this case we can derive the evolution equations using the mass
continuity equation and Newton's equation of the motion of a small
sphere. We have from the homogeneity assumption that

 = 0, from
isotropy that
= 0, from
isotropy that  . v = 3H(t) =
3
. v = 3H(t) =
3 / R and then
from
/ R and then
from 
 /
/
 t +
t +
 .
(
.
( v) = 0
we obtain:
v) = 0
we obtain:
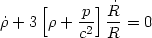
| (4) |
Rearranging (4) and using Newton's equation of motion,
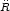 = -GM /
R2, we have:
= -GM /
R2, we have:
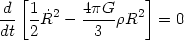
| (5) |
and integrating we obtain a Newtonian analogue of cosmological evolution equation:
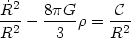
| (6) |
where  is the constant
of integration, which is closely related to
the Newtonian energy. We can see this if we rearrange (6) as:
is the constant
of integration, which is closely related to
the Newtonian energy. We can see this if we rearrange (6) as:
 2 / 2 -
GM/R = -
2 / 2 -
GM/R = -  /
2. Within the relativistic formulation, the constant
is in effect related to the curvature of space;
/
2. Within the relativistic formulation, the constant
is in effect related to the curvature of space;
 =
kc2 and the basic
equation of cosmological evolution, the Friedmann equation, is
written:
=
kc2 and the basic
equation of cosmological evolution, the Friedmann equation, is
written:
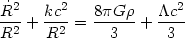
| (7) |
where the cosmological constant
( ) term was
introduced by Einstein
(rather ad hoc) in order to obtain his preferred static
solution. Given an equation of state, p =
p(
) term was
introduced by Einstein
(rather ad hoc) in order to obtain his preferred static
solution. Given an equation of state, p =
p( ),
we can solve for
),
we can solve for
 and then (7)
can be integrated to give R(t).
and then (7)
can be integrated to give R(t).
If we recall Newton's equation of motion,
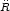 =
-GM / R2, and we use the active density (3) and (7), we
derive the second important dynamical
equation of cosmological evolution. The correct relativistic form of this
equation is:
=
-GM / R2, and we use the active density (3) and (7), we
derive the second important dynamical
equation of cosmological evolution. The correct relativistic form of this
equation is:
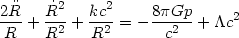
| (8) |
Equation of State: The question arises of which is the appropriate equation of state for the expanding Universe. The Universe expands adiabatically (1), since the symmetry imposed by the Cosmological principle implies that there is no net heat flow through any surface. Therefore as it expands, it cools (11) and since it started with a very hot phase, it will be dominated, at different epochs, by different species of particles having distinct equations of state. Relativistic particles will dominate the hot phase while non-relativistic the later cooler phases.
We can specify a unique equation of state p =
p( ) for
all epochs by parameterizing it according to:
) for
all epochs by parameterizing it according to:
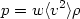
| (9) |
where <v2> is the velocity dispersion of the
fluid elements. If the
dominant contribution to the density comes from relativistic particles,
which have p = 1 /
3 c2 (when kT >> m0
v2, with v2
c2 (when kT >> m0
v2, with v2
 c2), then w = 1 / 3.
If the dominant contribution comes from non-relativistic matter (when
kT~ m0v2 with
v2 << c2) then there is
negligible pressure and the dust
approximation is excellent (w = 0).
c2), then w = 1 / 3.
If the dominant contribution comes from non-relativistic matter (when
kT~ m0v2 with
v2 << c2) then there is
negligible pressure and the dust
approximation is excellent (w = 0).
Therefore inserting (9) into the mass continuity equation, (4), we obtain:
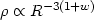
| (10) |
Armed with (10) one can now solve the Friedmann equation to get the time evolution of R(t), determine the age of the Universe, etc, in the different Cosmological models.
1 An adiabatic process is defined as that in which there is no heat flow and thus the entropy is conserved (dS = 0). Back.