3.1. The CMB fluctuation spectrum

The most straight forward approach to estimate the total matter and energy density of the Universe (ie., the total ) is by means of the measurement of the fluctuation spectrum of the CMB. Before recombination at z 1100, the baryons and photons are tightly coupled, oscillating acoustically due to gravity (on sub-horizon scales). Only after recombination do the acoustic oscillations stop and the density fluctuations grow. The fluctuations emerging from the last scattering surface are a series of peaks and troughs [169] and as the different wave-lengths are projected to different angular scales on the last scattering surface and depending on the underlying cosmological model, they produce a characteristic structure of peaks on the CMB power spectrum (for a recent review see [98] and references therein). This method is in effect based in measuring the angular extent of a physical scale on the last scattering surface. The curvature of space enters through the angular distance to the last scattering surface. Therefore, the same physical scale will be projected to a smaller angular scale on the CMB sky in a positively curved background, while it will be projected to a larger angular scale in a flat or to an even larger scale in a negatively curved background space.

To define the CMB power spectrum one starts by expanding the temperature fluctuations of the CMB sky in spherical harmonics:

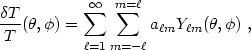
(64)

then if the fluctuations are Gaussian, the 2-point correlation function contains all the statistical information, and can be defined as:

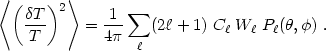
(65)

where W is the window function representing the beam characteristics of the experimental apparatus used to observe the CMB sky, while the average is over all positions on the sky. One then invokes the ergotic theorem, ie, that the above average is equivalent to being over different realizations of our Universe. Then assuming random phases one can define the CMB power spectrum C as the ensemble average of the coefficients a_m:

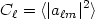
The different cosmological parameters will reflect onto a different structure of peaks in the structure of the CMB power spectrum. The position of the first peak is determined by the global mass/energy density of the Universe and the dependence of _peak on can be approximated by:

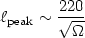
(66)

Note however, that this approximation is not correct in -dominated universes and small corrections should be applied (cf. [99]). Many recent experiments like the BOMMERANG, MAXIMA and DASI (cf. [44], [43], [90], [164], [130]) find:

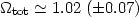
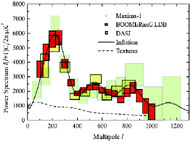
Many other cosmological parameters (for example _m, , H₀, baryon content of the universe, the spectral index n of the inflationary perturbation spectrum, etc) affect the structure of the peaks, beyond the first one (cf. [71]). Determining the CMB spectrum up to a few thousand 's can put strong constraints on these parameters. Current experiments trace the CMB spectrum up to ~ 1000 and indeed they have detected two more significant peaks at roughly ~ 540 and 840 [43] (see Fig.6).

Figure 6. CMB spectrum from the BOMMERANG, MAXIMA and DASI experiments with the error boxes of the measurements. The predictions of the popular inflationary model and one non-Gaussian (global texture) model (from [98] with permission).

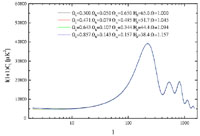
Note however, that different combinations of the cosmological parameters can conspire to produce exactly the same CMB spectrum; this is the so called degeneracy problem (see Fig.7) and therefore in order to provide limits to these cosmological parameters one needs to assume priors and/or constrain different combinations of these parameters. However, the more accurate the derived CMB spectrum the weaker the necessary priors ⁽²⁾.

Figure 7. Different combinations of the cosmological parameters can result in the same CMB power-spectrum - degeneracy problem (form [99] with permission).

The latest data and CMB spectrum analysis provides very stringent constraints to the baryon content of the Universe: _b h² 0.022_-0.003^+0.004, consistent with the primordial nucleosynthesis constraints (see 63), and to the spectral index of the power spectrum of primordial perturbations: n 0.96 ± 0.1 [43]. Furthermore, combined analyses with other cosmological data, can be used to break the above mentioned degenerecies (see below).

² With the new CMB experiments - MAP and PLANCK - the CMB power spectrum will be determined to an unprecedent detail, providing extremely accurate values for more than 10 cosmological parameters [160] Back.