3.4. M/L observations

Each astronomical object is characterized by a quantity called Mass-to-Light ratio, M/L. A convenient scaling of M/L is done by using the value of the solar neighbourhood, M / L. Then, observing M/L > M / L would imply the existence of DM of unknown composition and origin. Note that in most cases the evidence for M/L > M / L comes from the gravitational effects of the DM. Different classes of extragalactic objects (galaxies, clusters, etc) are characterized by different M/L, indicating that possibly a different fraction of the total mass of each type of object is Dark.

Estimating the universal luminosity density (see further below) and using the derived M/L values of each class of extragalactic object we can estimate its contribution to the total _m. Furthermore, if the estimated M/L is representative of the global universal value, then we can derive the overall value of _m.

I will present below the basic ideas behind the determination of M/L for the different extragalactic populations.

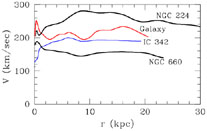
Spiral Galaxies: The Rotation curves of spirals (see Fig.10) are obtained by measuring Doppler-shifts of emission lines in HII regions, at radio wavelengths using the 21-cm emission line of neutral Hydrogen or using the CO-line and in the latter cases the rotation curve is measured at several times the optical radius of a galaxy (for a recent review see [162]).

Figure 10. Figure 10: Pie-diagram of the latest 2dF release, containing 160000 galaxies (with permission from the 2DFGRS TEAM).

One would expect the rotation curve to fall roughly as the surface brightness and beyond a few length-scales to fall as v_rot r^-1/2 (because most of the mass is rather centrally located) which is not observed. The rotation curves are found to be flat as far as they can be observed. From simple Newtonian Physics we have that:

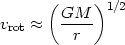
and since v_rot constant, we have that M(r) r, ie., mass increases linearly with distance beyond its optical radius, an indication for the presence of dark matter. The average value of M/L found for spiral galaxies out to ~ 20 kpc, is:

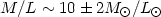
(75)

Figure 11. Rotation curves of 4 spiral galaxies, one of which is the Galaxy (data taken from [161]).

Note that the M/L value is an increasing function of outer radius, implying the existence of an extended dark matter halo (cf. [3]).

Elliptical Galaxies: In principle one can invoke a similar method with that of the spirals, if instead of the rotational velocity, the stellar velocity dispersion is used. The amplitude of this velocity measure is dictated by the gravitational potential of the elliptical and thus the virial theorem can be used to determine its total gravitating mass. However, stellar orbits are highly uncertain and the velocity dispersion ellipsoid may not be isotropic (see discussion in [16]).

Luckily, elliptical galaxies contain very hot gas (T ~ 5 × 10⁶ K) which emits X-rays. This gas constitutes about 10% of the observed mass in stars. For a spherically symmetric galaxy in hydrostatic equilibrium (v = 0) we have from Euler's equation that:

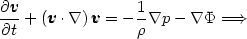
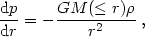
Using the ideal gas law (p = k_b T/m) with m the molecular mass and k_b the Boltzmann constant, we obtain that:

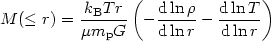
(76)

where T is the gas temperature, m_p is the proton mass and µ is the mean molecular weight. Therefore if we measure the temperature and density profiles we can find the total mass distribution M(< r). Finally the average mass-to-light ratio from this class of objects, out to ~ 20 kpc, is:

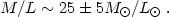
(77)

Groups of Galaxies: Groups of galaxies containing a few galaxies (3 - 10) are usually considered bound (due to the high density of galaxies). Then, according to the Virial theorem (2T + U = 0), a group with N galaxies having velocity and position vectors (relative to the centre of mass of the group) v_i and r_i respectively, has:

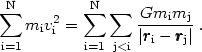
However what we measure is not v_i but only the line-of-sight component of the the velocity u_i. Assuming isotropic orbits then v_i² 3<u_i²>. Assuming that the mass-to-light ratio of each member galaxy is the same, m_i / L_i = M/L, we obtain:

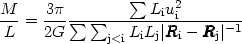
(78)

where |R_i - R_j| is the projection of |r_i - r_j| on the plane of the sky.

However this measure should be used only if N is large, or otherwise statistically, ie, averaged over a large number of groups to find the <M/L> of the ensemble. Note that this estimator is very sensitive to the group-finding algorithm, selection procedure, selection function corrections (ie., corrections to take into account the fact that the galaxy density artificially decreases with depth in magnitude/flux limited samples). Furthermore, projection effects (ie; inclusion in the group of a foreground or background galaxy) is also a source of error. For example the inclusion of a non-member would result in an artificially higher M/L while conversely the exclusion of a member (due to a high u_i) would underestimate the M/L.

The mass-to-light ratio for groups of galaxies (cf. [132]) is:

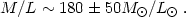
(79)

Clusters of Galaxies: The most common approach to measure the cluster M/L is based on the assumption that clusters are in virial equilibrium, for which we do have strong indications.

The first step in determining M/L is to measure the cluster velocity dispersion accurately. Using the recent compilation of 395 R 0 ABELL/ACO cluster velocity dispersions [167] I find:

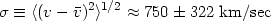
However, this value is based even on clusters for which the velocity dispersion was determined from a very small number of galaxy redshifts, a fact which increases the possibility of assigning an erroneous -value. This can be seen in the left panel of Fig. 11 were we plot the normalized frequency distribution for clusters with N_z < 20 and N_z > 20. The skewed distribution to large -values for N_z < 20 is evident, while the mean -value is smaller than for the N_z > 20 case. As a compromise between having enough redshifts per cluster, in order to get a reliable -value, and a large cluster sample, we choose those with N_z > 20. For these 195 clusters I find that:

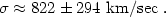
A consistent value of 940 ± 208 km/sec has been found from the 16 high-redshift clusters of the CNOC project [32] and a variety of methods used to define cluster membership and account for interlopers [23].

Now from the Virial theorem, m = 2² r_a / G, we have:

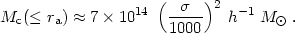
(80)

where r_a = 1.5 h^-1 Mpc. Using a number-galaxy weighted luminosity estimation, and assuming an average cluster value in the optical of L 10¹² h^-2 L (cf. [4]), we obtain the distribution of M/L values (see right panel of Fig. 11). Since the distribution is non-Gaussian we quote below the median and 68% confidence levels:

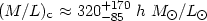
(81)

A more accurate method that can be used to estimate cluster mass is based on the measurements of the X-ray emission from the ICM gas, similar to the method used for individual elliptical galaxies (76). Although not strictly correct, usually an isothermal cluster profile is used (d ln T / d ln r = 0), which greatly simplifies calculations. However, recent experiments have shown that indeed the cluster Temperature does not vary significantly with radius (d ln T / d ln r -0.7 ~ -0.8). Estimates of M/L derived with this method are in general agreement with (81).

Global luminosity density and _m: We estimate the value of <L> using the galaxy luminosity function which is defined such that (L)dL is the number density of galaxies having total luminosity in the interval (L, L + dL). A good fit to the observed luminosity function of the field population of galaxies is provided by the Schechter function [153]:

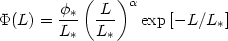
(82)

where = -1.29 ± 0.11, _* = 1.3 ± 0.3 × 10^-2h³ Mpc^-3 and L_* = 1.1 × 10¹⁰ h^-2 L (see also [52]). Then the mean luminosity density, corresponding to (82), is:

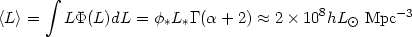
(83)

Using the value of _cr (15) we have:

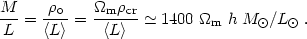
(84)

In Table 2 we summarize the <M/L> values found at different scales and the corresponding contribution to _m.

Since galaxy clusters are the deepest potential wells in the Universe and they accumulate baryonic and DM from large volumes, it is expected that their M/L ratio could represent the Universal value. This view is supported by the fact that the increasing trend of M/L with scale (seen in Table 2) reaches a plateau at the corresponding value of the clusters (cf. [3], [6]). Therefore the universal value, as given by the clusters is:

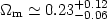
The analysis of the CNOC sample of 16 distant clusters (0.17 < z < 0.55), provides a consistent value but with significantly smaller uncertainty; _m 0.19 ± 0.06 (see [32] and references therein).

Table 2. Mass-to-light ratios and contribution to _m for the different scales.

Object	scale (h-1 Mpc)	<M/L > h-1	m
Spirals	0.02	10±2	0.0071 ±0.0015
Ellipticals	0.02	25±5	0.018±0.004
Galaxy pairs	0.1	80±20	0.057±0.012
Groups	0.8	180±60	0.13±0.09
Clusters	1.5	320+170-85	0.23+0.12-0.06