


3.3. Clustering of Galaxies, Clusters & QSO's
If we assume a
continuous density field of extragalactic objects,
 (r),
with mean
(r),
with mean  , we
define the fluctuations of the field at position x as:
, we
define the fluctuations of the field at position x as:
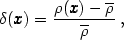
| (67) |
Obviously we have that
< (x)> =
0. The correlation function is defined as:
(x)> =
0. The correlation function is defined as:
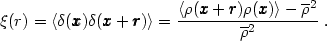
| (68) |
and quantifies the extend to which the density fluctuations at a given point are correlated to those at a distance r. The value of 2-point correlation function at zero-lag is therefore the variance of the random process:
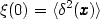
|
which measures the excursions of the density about its mean value.
However, this is not a well defined quantity because usually the
fluctuation field is smoothed to some resolution, say R. We then
evaluate the variance of this field as r
 0 (see 71 below).
0 (see 71 below).
In many problems it is convenient to work in wave-number space.
The Fourier transform of
 (x) is:
(x) is:
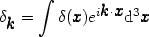
| (69) |
and it is convenient to separate
 k in
modulus and argument:
k in
modulus and argument:
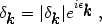
|
where
 k
are the phases (usually assumed to be randomly distributed in
[0,
k
are the phases (usually assumed to be randomly distributed in
[0,  ), although the non-linear
evolution of structure introduces phase correlations, cf.
[33]).
The variance of the amplitudes is the power spectrum:
), although the non-linear
evolution of structure introduces phase correlations, cf.
[33]).
The variance of the amplitudes is the power spectrum:
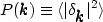
|
which is the Fourier transform of the correlation function (Wiener-Khinchin theorem):
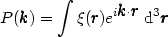
| (70) |
and with inverse transform:
 (r) =
(2
(r) =
(2 )-3
)-3
 P(k)
e-ik .r d3 k.
At the origin r = 0 we obtain
P(k)
e-ik .r d3 k.
At the origin r = 0 we obtain
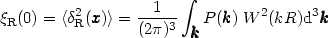
| (71) |
where w is the window function function that reflects the filtering of the field. The power spectrum is the contribution of modes of wavenumber k to the total variance, per unit volume of wavenumber space. If the fluctuation field is a Gaussian Random Field, then the power-spectrum contains all the statistical information of the fluctuations. A similar formulation is applicable also in the two dimensional case (where the density field is on the surface of a sphere - the sky). Only that instead of the Fourier transform we use the Spherical Harmonic transform.
Although I will not enter in the details of how to estimate the power spectrum of some distribution of extragalactic objects, I will only note that a good estimation of the window function (containing the survey boundaries, obscuration, radial selection function and instrumental biases for example) is necessary in order to get a reliable power-spectrum determination.
A further ingredient that complicates considerably matters is the so
called biasing of the galaxies, or in general of any mass-tracer
population, with respect to mass
[79].
The usual relation, assumed between the mass-tracer fluctuations
( tr) and the
underline mass
fluctuation field, is encapsulated in the bias factor b:
tr) and the
underline mass
fluctuation field, is encapsulated in the bias factor b:
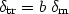
| (72) |
and therefore we have that the galaxy (tracer) power spectrum is
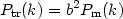
|
It has been shown that the linear biasing model (72) is a good approximation, at least on scales were non-linear gravitational effects are weak (see [106] and references therein).
Within the inflationary paradigm the initial fluctuations, in the early universe, that gave rise to the observed large-scale structure today, are adiabatic and Gaussian and therefore one can characterize these fluctuations completely using the above tools. The power spectrum of such initial fluctuations is:
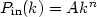
|
usually with n = 1 (Harrison-Zeldovich spectrum), and A its amplitude. The different fluctuation damping mechanisms, operating during the radiation dominated area, modify Pin(k). These effects can be encapsulated in the transfer function, t (k) and today's linear fluctuation spectrum has the form [8]:
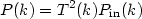
|
In the linear regime (while fluctuations << 1) the power spectrum shape is preserved, because each Fourier mode evolves independently.
I will now concentrate on a few methods, based on the clustering of galaxies and QSO's, and I will present only very recent results. The subject is extremely rich, many have laboriously worked towards attaining the goal of pining down the different cosmological parameters and I hope that they will forgive me for not being able to mention the vast literature on the subject.
The Shape of p (k): The
popular Cold Dark Matter (CDM)
model has a T (k) parametrised by the so-called
shape-parameter,
 ,
which characterizes the shape of the p (k) and has the form
[168]:
,
which characterizes the shape of the p (k) and has the form
[168]:
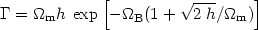
| (73) |
We see that measuring the the power-spectrum of extragalactic
populations and estimating
 we can put
constraints on the combination of the cosmological parameters:
we can put
constraints on the combination of the cosmological parameters:
 m and
h
(
m and
h
( b
affects weakly
b
affects weakly  ).
).
The recent 2dF survey [37] has measured already measured more than 160000 galaxy and 10000 QSO redshifts, which constitute it the largest spectroscopic catalogue of extragalactic objects.
A number of recent papers have estimated the galaxy and QSO
power-spectra providing important constraints on the
 parameter. From
the p (k) of galaxies
[117]
it was found that there is a degeneracy between the
parameter. From
the p (k) of galaxies
[117]
it was found that there is a degeneracy between the
 m
h and
m
h and
 b /
b /
 m, which
if broken (using the CMB or BBN
results) provide the following constraints:
m, which
if broken (using the CMB or BBN
results) provide the following constraints:
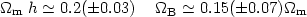
|
which for h = 0.72 means that
 m =
0.28. The analysis of the QSO p (k)
[70]
showed a somewhat smaller value but still consistent within the
statistical uncertainties:
m =
0.28. The analysis of the QSO p (k)
[70]
showed a somewhat smaller value but still consistent within the
statistical uncertainties:
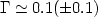
|
Similar results come from the SSDS photometric survey [165] which contains 1.5 × 106 galaxies with redshifts up to ~ 0.4. The angular power-spectrum analysis, after inverting to 3D using Limber's integral equation, give [47], [170]:
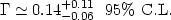
|
Obviously, all these results support a low
 m universe.
m universe.
Redshift Space Distortions: As we have already discussed in section 2, the measured expansion velocity of an extragalactic object contains also the contribution of the local gravitational field. The peculiar velocities will distort the apparent 3D distribution of the extragalactic objects, a fact which will manifest itself in the 2-point correlation function, when plotted as a function of the transverse and radial pair separation. The redshift space correlation function is related to the real space, under a few assumptions; see [78], according to:
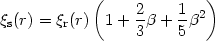
| (74) |
where  =
=
 m0.6 / b. By estimating the
angular power-spectrum,
C
m0.6 / b. By estimating the
angular power-spectrum,
C , or
its Fourier transform
w(
, or
its Fourier transform
w( ), and then
inverting it to 3D via Limber's
equation, one has an unaffected, by redshift space distortions, measure of
these parameters. Then using (74) and the measured
), and then
inverting it to 3D via Limber's
equation, one has an unaffected, by redshift space distortions, measure of
these parameters. Then using (74) and the measured
 s(r) one can place constraints on
s(r) one can place constraints on
 . Such an
analysis of the 2dF galaxy survey gave
[113]:
. Such an
analysis of the 2dF galaxy survey gave
[113]:
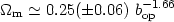
|
A subsequent analysis, using a different method, provided very similar results [172]:
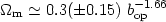
|
The corresponding QSO survey
[108]
did not provide very stringent
constraints (ie., the EdS model was rejected only at a
1.4 level),
however their best fit gives:
level),
however their best fit gives:
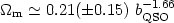
|
Joint Likelihoods: Alot of recent interest was generated by the understanding that joining the analyses of different data sets, one may break the degeneracies between the different cosmological parameters (cf. [182], [53], [29], [181]). Especially joining the CMB, SNIa and large-scale clustering results may lead to strong constraints on more than 8 cosmological parameters (see however [87] for many subtleties involved).
The joint analysis
[54]
of the 2dF galaxy p (k) and the CMB data have
provided another strong indication for a positive cosmological constant,
independent of the SNIa results, with a
2 range:
range:
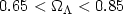
|
Furthermore, some of the other constraints are: 0.17 <
 m <
0.31 for h = 0.72, 0.6 < h < 0.86.
m <
0.31 for h = 0.72, 0.6 < h < 0.86.