11. The anisotropy of the cosmic microwave background radiation

The wonderfully successful CDM prediction of the power spectrum of the angular distribution of the temperature of the 3 K cosmic microwave background radiation has converted many of the remaining skeptics in the cosmology community to the belief that the CDM model likely does capture important elements of reality.

Efstathiou (2002) provides a useful measure of the information in the present measurements ⁽⁹⁰⁾: the fit to the CDM model significantly constrains three linear combinations of the free parameters. We shall present three sets of considerations that roughly follow Efstathiou's constraints. We begin with reviews of the standard measure of the temperature anisotropy and of the conditions at redshift z ~ 1000 that are thought to produce the observed anisotropy.

The 3 K cosmic microwave background temperature T(, ) as a function of position in the sky usually is expressed as an expansion in spherical harmonics,

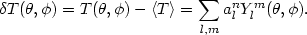(77)

The square of T averaged over the sky is

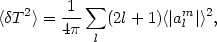(78)

where |a_l^m|² is statistically independent of m. This may be rewritten as

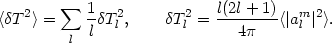(79)

Since l^-1 is close to d ln l, T_l² is the variance of the temperature per logarithmic interval of l. A measure of the angular scale belonging to the multipole index l is that the minimum distance between zeros of the spherical harmonic Y_l^m, in longitude or latitude, is = / l, except close to the poles, where Y_l^m approaches zero. ⁽⁹¹⁾

Now let us consider the main elements of the physics that determines the 3 K cosmic microwave background anisotropy. ⁽⁹²⁾ At redshift z_dec ~ 1000 the temperature reaches the critical value at which the primeval plasma combines to atomic hydrogen (and slightly earlier to neutral helium). This removes the coupling between baryons and radiation by Thomson scattering, leaving the radiation to propagate nearly freely (apart from residual gravitational perturbations). Ratios of mass densities near the epoch z_dec when matter and radiation decouple are worth noting. At redshift z_eq = 2.4 × 10⁴ _M0 h² the mass density in matter - including the baryonic and nonbaryonic components - is equal to the relativistic mass density in radiation and neutrinos assumed to have low masses. At decoupling the ratio of mass densities is

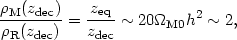(80)

at the central values of the parameters in Eqs. (6) and (59). The ratio of mass densities in baryons and in thermal cosmic microwave background radiation - not counting neutrinos - is

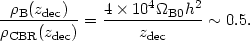(81)

That is, the baryons and radiation decouple just as the expansion rate has become dominated by nonrelativistic matter and the baryons are starting to lower the velocity of sound in the coupled baryon-radiation fluid (presenting us with still more cosmic coincidences).

The acoustic peaks in the spectrum of angular fluctuations of the 3 K cosmic microwave background radiation come from the Fourier modes of the coupled baryon-radiation fluid that have reached maximum or minimum amplitude at decoupling. Since all Fourier components start at zero amplitude at high redshift - in the growing density perturbation mode - this condition is

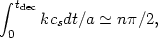(82)

where c_s is the velocity of sound in the baryon-radiation fluid. Before decoupling the mass density in radiation is greater than that of the baryons, so the velocity of sound is close to c / 3^1/2. The proper wavelength at the first acoustic peak thus is

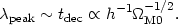(83)

The parameter dependence comes from Eq. (66). The observed angle subtended by _peak is set by the angular size distance r computed from z_eq to the present (Eq. [71]). If _K0 = 0 or ₀ = 0 the angular size distance is

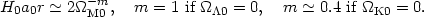(84)

If = 0 this expression is analytic at large z_eq. The expression for _K0 = 0 is a reasonable approximation to the numerical solution. So the angular scale of the peak varies with the matter density parameter as

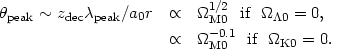(85) (86)

The key point from these considerations is that the angle defined by the first peak in the fluctuation power spectrum is sensitive to _M0 if = 0 (Eq. [85]), but not if _K0 = 0 (Eq. [86]). ⁽⁹³⁾ We have ignored the sensitivity of z_dec and t_dec to _M0, but the effect is weak. More detailed computations, which are needed for a precise comparison with the data, show that the CDM model predicts that the first and largest peak of T_l appears at multipole index l_peak 220_M0^-1/2 if = 0, and at l_peak 220 if _K0 = 0 and 0.1 _M0 1. ⁽⁹⁴⁾

The measured spectrum ⁽⁹⁵⁾ peaks at T_l ~ 80 µK at l ~ 200, thus requiring small space curvature in the CDM model. This is the first of Efstathiou's constraints. Because of the geometric degeneracy this measurement does not yet seriously constrain _M0 if _K0 = 0.

The second constraint comes from the spectrum of temperature fluctuations on large scales, l 30, where pressure gradient forces never were very important. Under the scale-invariant initial conditions discussed in Sec. III.C the Einstein-de Sitter model predicts T_l is nearly independent of l on large scales. A spatially-flat model with _M0 ~ 0.3, predicts T_l decreases slowly with increasing l at small l. ⁽⁹⁶⁾ The measured spectrum is close to flat at T_l ~ 30 µK, but not well enough constrained for a useful measure of the parameters _M0 and ₀. ⁽⁹⁷⁾ Because of the simplicity of the physics on large angular scales, this provides the most direct and so perhaps most reliable normalization of the CDM model power spectrum (that is, the parameter A in Eqs. [40] and [41]).

The third constraint is the baryon mass density. It affects the speed of sound c_s (Eq. [82]) in the baryon-radiation fluid prior to decoupling, and the mean free path for the radiation at z ~ z_dec. These in turn affect the predicted sequence of acoustic peaks (see, e.g., Hu and Sugiyama, 1996). The detected peaks are consistent with a value for the baryon density parameter _B0 in a range that includes what is derived from the light elements elements abundances (Eqs. [62]). ⁽⁹⁸⁾ This impressive check may be much improved by the measurements of T_l in progress.

The measurements of T_l are consistent with a near scale-invariant power spectrum (Eq. [41] with n 1) with negligible contribution from gravity wave or isocurvature fluctuations (Sec. III.C.1). The 3 K cosmic microwave background temperature fluctuations show no departure from a Gaussian random process. ⁽⁹⁹⁾ This agrees with the picture in test (10) for the nonlinear growth of structure out of Gaussian initial mass density fluctuations.

The interpretation of the cosmic microwave background temperature anisotropy measurements assumes and tests general relativity and the CDM model. One can write down other models for structure formation that put the peak of T_l at about the observed angular scale - an example is Hu and Peebles (2000) - but we have seen none so far that seem likely to fit the present measurements of T_l. Delayed recombination of the primeval plasma in an low density = 0 CDM model can shift the peak of T_l to the observed scale. ⁽¹⁰⁰⁾ The physics is valid, but the scenario is speculative and arguably quite improbable. On the other hand, we cannot be sure a fix of the challenges to CDM reviewed in Sec. IV.A.2 will not affect our assessments of such issues, and hence of this cosmological test.

⁹⁰ Recent measurements are presented in Lee et al. (2001), Netterfield et al. (2002), Halverson et al. (2002), Miller et al. (2002a), Coble et al. (2001), Scott et al. (2002), and Mason et al. (2002). Back.

⁹¹ A more careful analysis distinguishes averages across the sky from ensemble averages. By historical accident the conventional normalization replaces 2l + 1 with 2(l + 1) in Eq. (79). Kosowsky (2002) reviews the physics of the polarization of the radiation. Back.

⁹² The physics is worked out in Peebles and Yu (1970) and Peebles (1982). Important analytic considerations are in Sunyaev and Zel'dovich (1970). The relation of the cosmic microwave background anisotropy to the cosmological parameters is explored in many papers; examples of the development of ideas include Bond (1988), Bond et al. (1994), Hu and Sugiyama (1996), Ratra et al. (1997, 1999), Zaldarriaga, Spergel, and Seljak (1997), and references therein. Back.

⁹³ This "geometrical degeneracy" is discussed by Efstathiou and Bond (1999). Marriage (2002) presents a closer analysis of the effect. Sugiyama and Gouda (1992), Kamionkowski, Spergel, and Sugiyama (1994b), and Kamionkowski et al. (1994a) are early discussions of the cosmic microwave background anisotropy in an open model. Back.

⁹⁴ Brax et al. (2000) and Baccigalupi et al. (2000) compute the angular spectrum of the cosmic microwave background anisotropy in the dark energy scalar field model. Doran et al. (2001) discuss the angular scale of the peaks in this case, and Corasaniti and Copeland (2002), Baccigalupi et al. (2002), and references therein, compare model predictions and observations - it is too early to draw profound conclusions about model viability, and new data are eagerly anticipated. Wasserman (2002) notes that the cosmic microwave background anisotropy data could help discriminate between different dark energy scalar field models whose predictions do not differ significantly at low redshift. Back.

⁹⁵ For analyses see Knox and Page (2000), Podariu et al. (2001), Wang, Tegmark, and Zaldarriaga (2002), Durrer, Novosyadlyj, and Apunevych (2001), Miller et al. (2002b), and references therein. Back.

⁹⁶ The physics was first demonstrated by Sachs and Wolfe (1967) and applied in the modern context by Peebles (1982). The intermediate Sachs-Wolfe effect that applies if the universe is not Einstein-de Sitter is shown in Eq. (93.26) in Peebles (1980). This part of the Sachs-Wolfe effect receives a contribution from the low redshift matter distribution, so cross-correlating the observed large-scale cosmic microwave background anisotropy with the low redshift matter distribution could provide another test of the world model (Boughn and Crittenden, 2001, and references therein). Back.

⁹⁷ See, e.g., Górski et al. (1998). This ignores the "low" value of the cosmological quadrupole (l = 2) moment, whose value depends on the model used to remove foreground Galactic emission (see, e.g., Kogut et al., 1996). Contamination due to non-cosmic microwave background emission is an issue for some of the anisotropy data sets (see, e.g., de Oliveira-Costa et al., 1998; Hamilton and Ganga, 2001; Mukherjee et al., 2002, and references therein). Other issues that need care in such analyses include accounting for the uncertainty in the calibration of the experiment (see, e.g., Ganga et al., 1997; Bridle et al., 2001), and accounting for the shape of the antenna pattern (see, e.g., Wu et al., 2001a; Souradeep and Ratra, 2001; Fosalba, Dore, and Bouchet, 2002). Back.

⁹⁸ The _B0 h² values estimated from the cosmic microwave background anisotropy measured by Netterfield et al. (2002), Pryke et al. (2002), and Stompor et al. (2001), are more consistent with the higher, deuterium based, Burles et al. (2001) range in Eqs. (62). Back.

⁹⁹ Colley, Gott, and Park (1996) present an early discussion of the situation on large angular scales; more recent discussions are in Mukherjee, Hobson, and Lasenby (2000), Phillips and Kogut (2001), and Komatsu et al. (2002). Degree and sub-degree angular scale anisotropy data are studied in Park et al. (2001), Wu et al. (2001b), Shandarin et al. (2002), and Polenta et al. (2002). Back.

¹⁰⁰ The model in Peebles, Seager, and Hu (2000) assumes stellar ionizing radiation at z ~ 1000 produces recombination Lyman photons. These resonance photons promote photoionization from the n = 2 level of atomic hydrogen. That allows delayed recombination with a rapid transition to neutral atomic hydrogen, as required to get the shape of T_l about right. Back.