


4. The redshift-angular size and redshift-magnitude relations
An object at redshift z with physical length l perpendicular
to the line of sight subtends angle
 such that
such that
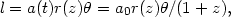 |
(69) |
where a0 = a(t0). The angular size distance r(z) is the coordinate position of the object in the first line element in Eq. (15), with the observer placed at the origin. The condition that light moves from source to observer on a radial null geodesic is
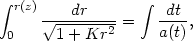 |
(70) |
which gives
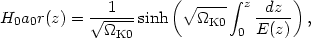 |
(71) |
where E(z) is defined in Eqs. (11) and (65).
In the Einstein-de Sitter model, the angular-size-redshift relation is
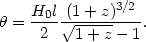 |
(72) |
At z << 1,  =
H0l / z, consistent with the Hubble
redshift-distance relation. At z >> 1 the image is
magnified, (73)
=
H0l / z, consistent with the Hubble
redshift-distance relation. At z >> 1 the image is
magnified, (73)

 1 + z.
1 + z.
The relation between the luminosity of a galaxy and the energy
flux density received by an observer follows from Liouville's
theorem: the observed energy flux
i 0
per unit time, area, solid angle, and frequency satisfies
0
per unit time, area, solid angle, and frequency satisfies
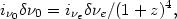 |
(73) |
with
i e
the emitted energy flux (surface brightness)
at the source and
e
the emitted energy flux (surface brightness)
at the source and 
 e =
e =

 0(1 + z) the
bandwidth at the source at redshift z. The redshift factor (1 +
z)4
appears for the same reason as in the 3 K cosmic microwave
background radiation energy density. With Eq. (69) to
fix the solid angle, Eq. (73) says
the observed energy flux per unit area, time, and
frequency from a galaxy at redshift z that has luminosity
L
0(1 + z) the
bandwidth at the source at redshift z. The redshift factor (1 +
z)4
appears for the same reason as in the 3 K cosmic microwave
background radiation energy density. With Eq. (69) to
fix the solid angle, Eq. (73) says
the observed energy flux per unit area, time, and
frequency from a galaxy at redshift z that has luminosity
L e
per frequency interval measured at the source is
e
per frequency interval measured at the source is
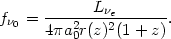 |
(74) |
In conventional local physics with a single metric theory the redshift-angular size (Eq. [69]) and redshift-magnitude (Eq. [74]) relations are physically equivalent. (74)
The best present measurement of the redshift-magnitude relation
uses supernovae of Type Ia.
(75)
The results are inconsistent with the Einstein-de
Sitter model, at enough standard deviations to make it clear
that unless there is something quite substantially and
unexpectedly wrong with the measurements the Einstein-de Sitter
model is ruled out. The data require
 > 0 at two to
three standard deviations,
depending on the choice of data and method of analysis
(Leibundgut, 2001;
Gott et al., 2001).
The spatially-flat case with
> 0 at two to
three standard deviations,
depending on the choice of data and method of analysis
(Leibundgut, 2001;
Gott et al., 2001).
The spatially-flat case with
 M0 in the
range of Eq. (59) is a good fit for
constant
M0 in the
range of Eq. (59) is a good fit for
constant  .
The current data do not provide interesting
constraints on the models for evolving dark energy
density. (76)
Perlmutter et al.
(http://snap.lbl.gov/)
show that a
tighter constraint, from supernovae observations to redshift z ~ 2,
by the proposed SNAP satellite, is feasible and capable of giving
a significant detection of
.
The current data do not provide interesting
constraints on the models for evolving dark energy
density. (76)
Perlmutter et al.
(http://snap.lbl.gov/)
show that a
tighter constraint, from supernovae observations to redshift z ~ 2,
by the proposed SNAP satellite, is feasible and capable of giving
a significant detection of
 and maybe its
evolution. (77)
and maybe its
evolution. (77)
73 The earliest discussion we know of the magnification effect is by Hoyle (1959). In the coordinate system in Eq. (15), with the observer at the origin, light rays from the object move to the observer along straight radial lines. An image at high redshift is magnified because the light detected by the observer is emitted when the proper distance to the object measured at fixed world time is small. Because the proper distance between the object and source is increasing faster than the speed of light, emitted light directed at the observer is initially moving away from the observer. Back.
74 For a review of measurements of the redshift-magnitude relation (and other cosmological tests) we recommend Sandage (1988). A recent application to the most luminous galaxies in clusters is in Aragón-Salamanca, Baugh, and Kauffmann (1998). The redshift-angular size relation is measured by Daly and Guerra (2001) for radio galaxies, Buchalter et al. (1998) for quasars, and Gurvits, Kellermann, and Frey (1999) for compact radio sources. Constraints on the cosmological parameters from the Gurvits et al. data are discussed by Vishwakarma (2001), Lima and Alcaniz (2002), Chen and Ratra (2002), and references therein, and constraints based on the radio galaxy data are discussed by Daly and Guerra (2001), Podariu et al. (2002), and references therein. Back.
75 These supernovae are characterized by the absence of hydrogen lines in the spectra; they are thought to be the result of explosive nuclear burning of white dwarf stars. Pskovskii (1977) and Phillips (1993) pioneered the reduction of the supernovae luminosities to a near universal standard candle. For recent discussions of their use as a cosmological test see Goobar and Perlmutter (1995), Reiss et al. (1998), Perlmutter et al. (1999a), Gott et al. (2001), and Leibundgut (2001). We recommend Leibundgut's (2001) cautionary discussion of astrophysical uncertainties: the unknown nature of the trigger for the nuclear burning, the possibility that the Phillips correction to a fiducial luminosity actually depends on redshift or environment within a galaxy, and possible obscuration by intergalactic dust. There are also issues of physics that may affect this test (and others): the strengths of the gravitational or electromagnetic interactions may vary with time, and photon-axion conversion may reduce the number of photons reaching us. All of this is under active study. Back.
76 Podariu and Ratra (2000) and Waga and Frieman (2000) discuss the redshift-magnitude relation in the inverse power-law scalar field model, and Waga and Frieman (2000) and Ng and Wiltshire (2001) discuss this relation in the massive scalar field model. Back.
77 Podariu, Nugent, and Ratra (2001), Weller and Albrecht (2002), Wang and Lovelace (2001), Gerke and Efstathiou (2002), Eriksson and Amanullah (2002), and references therein, discuss constraints on cosmological parameters from the proposed SNAP mission. Back.