7. Dynamics and the mean mass density

Estimates of the mean mass density from the relation between the mass distribution and the resulting peculiar velocities, ⁽⁷⁸⁾ and from the gravitational deflection of light, probe gravity physics and constrain _M0. The former is not sensitive to _K0, ₀, or the dynamics of the dark energy, the latter only through the angular size distances.

We begin with the redshift space of observed galaxy angular positions and redshift distances z/H₀ in the radial direction. The redshift z has a contribution from the radial peculiar velocity, which is a probe of the gravitational acceleration produced by the inhomogeneous mass distribution. The two-point correlation function, _v, in redshift space is defined by the probability that a randomly chosen galaxy has a neighbor at distance r_|| along the line of sight in redshift space and perpendicular distance r,

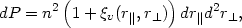(76)

where n is the galaxy number density. This is the usual definition of a reduced correlation function. Peculiar velocities make the function anisotropic. On small scales the random relative peculiar velocities of the galaxies broaden _v along the line of sight. On large scales the streaming peculiar velocity of convergence to gravitationally growing mass concentrations flattens _v along the line of sight. ⁽⁷⁹⁾

At 10kpc hr 1 Mpc the measured line-of-sight broadening is prominent, and indicates the one-dimensional relative velocity dispersion is close to independent of r at ~ 300 km s^-1. ⁽⁸⁰⁾ This is about what would be expected if the mass two-and three-point correlation functions were well approximated by the galaxy correlation functions, the mass clustering on these scales were close to statistical equilibrium, and the density parameter were in the range of Eq. (59).

We have a check from the motions of the galaxies in and around the Local Group of galaxies, where the absolute errors in the measurements of galaxy distances are least. The two largest group members are the Andromeda Nebula (M 31) and our Milky Way galaxy. If they contain most of the mass their relative motion is the classical two-body problem in Newtonian mechanics (with minor corrections for , mass accretion at low redshifts, and the tidal torques from neighboring galaxies). The two galaxies are separated by 800 kpc and approaching at 110 km s^-1. In the minimum mass solution the galaxies have completed just over half an orbit in the cosmological expansion time t₀ ~ 10¹⁰ yr. By this argument Kahn and Woltjer (1959) find the sum of masses of the two galaxies has to be an order of magnitude larger than what is seen in the luminous parts. An extension to the analysis of the motions and distances of the galaxies within 4 Mpc distance from us, and taking account of the gravitational effects of the galaxies out to 20 Mpc distance, gives masses quite similar to what Kahn and Woltjer found, and consistent with _M0 in the range of Eq. (59) (Peebles et al., 2001).

We have another check from weak lensing: the shear distortion of images of distant galaxies by the gravitational deflection by the inhomogeneous mass distribution. ⁽⁸¹⁾ If galaxies trace mass these measurements say the matter density parameter measured on scales from about 1 Mpc to 10 Mpc is in the range of Eq. (59). It will be interesting to see whether these measurements can check the factor of two difference between the relativistic gravitational deflection of light and the naive Newtonian deflection angle.

The redshift space correlation function _v (Eq. [76]) is measured well enough at hr ~ 10 Mpc to demonstrate the flattening effect, again consistent with _M0 in the range of Eq. (59), if galaxies trace mass. Similar numbers follow from galaxies selected as far infrared IRAS sources (Tadros et al., 1999) and from optically selected galaxies (Padilla et al., 2001; Peacock et al., 2001). The same physics, applied to estimates of the mean relative peculiar velocity of galaxies at separations ~ 10 Mpc, yet again indicates a similar density parameter (Juszkiewicz et al., 2000).

Other methods of analysis of the distributions of astronomical objects and peculiar velocities smoothed over scales 10 Mpc give a variety of results for the mass density, some above the range in Eq. (59), ⁽⁸²⁾ others towards the bottom end of the range (Branchini et al., 2001). The measurement of _M0 from large-scale streaming velocities thus remains open. But we are impressed by an apparently simple local situation, the peculiar motion of the Local Group toward the Virgo cluster of galaxies. This is the nearest known large mass concentration, at distance ~ 20 Mpc. Burstein (2000) finds that our virgocentric velocity is v_v = 220 km s^-1, indicating _M0 0.2 (Davis and Peebles, 1983a, Fig. 1). This leads us to conclude that the weight of the evidence from dynamics on scales ~ 10 Mpc favors low _M0, in the range of Eq. (59).

None of these measurements is precise. But many have been under discussion for a long time and seem to us to be reliably understood. Weak lensing is new, but the measurements are checked by several independent groups. The result, in our opinion, is a well checked and believable network of evidence that over two decades of well-sampled length scales, 100 kpc to 10 Mpc, the apparent value of _M0 is constant to a factor of three or so, in the range 0.15 _M0 0.4. The key point for the purpose of this review is that this result is contrary to what might have been expected from biasing, or from a failure of the inverse square law (as will be discussed in test [13]).

⁷⁸ Early estimates of the mean mass density, by Hubble (1936, p. 189) and Oort (1958), combine the galaxy number density from galaxy counts with estimates of galaxy masses from the internal motions of gas and stars. Hubble (1936, p. 180) was quite aware that this misses mass between the galaxies, and that the motions of galaxies within clusters suggests there is a lot more intergalactic mass (Zwicky, 1933; Smith, 1936). For a recent review of this subject see Bahcall et. al. (2000). Back.

⁷⁹ This approach grew out of the statistical method introduced by Geller and Peebles (1973); it is derived in its present form in Peebles (1980b) and first applied to a serious redshift sample in Davis and Peebles (1983b). These references give the theory for the second moment ² of _v in the radial direction - the mean square relative peculiar velocity - in the small-scale stable clustering limit. The analysis of the anisotropy of _v in the linear perturbation theory of large-scale flows (Eq. [55]) is presented in Kaiser (1987). Back.

⁸⁰ This measurement requires close attention to clusters that contribute little to the mean mass density but a broad and difficult to measure tail to the distribution of relative velocities. Details may be traced back through Padilla et al. (2001), Peacock et al. (2001), and Landy (2002). Back.

⁸¹ Recent studies include Wilson, Kaiser, and Luppino (2001), Van Waerbeke et al. (2002), Refregier, Rhodes, and Groth (2002), Bacon et al. (2002), and Hoekstra, Yee, and Gladders (2002). See Munshi and Wang (2002) and references therein for discussions of how weak lensing might probe dark energy. Back.

⁸² The methods and results may be traced through Fisher, Scharf, and Lahav (1994), Sigad et al. (1998), and Branchini et al. (2000). Back.