0A homogeneous and isotropic universe is characterized by the Friedmann-Robertson-Walker line element
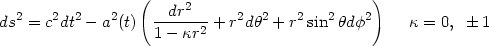
| (2) |
In this metric the Einstein equations (1) with matter in the form of a perfect fluid acquire the following simple form
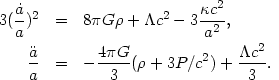
| (3) (4) |
Equation (4) can be recast to look like the equation of
motion of a point particle on the surface of a sphere of radius
R 
a and
mass M, setting c = 1 we obtain
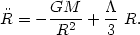
| (5) |
The total `gravitating mass'
M = 4
/ 3
R3(
+ 3P) reflects the fact that
`pressure carries weight' in Einstein's theory of gravity.
From (5) we find that a particle on the sphere feels both attractive
and repulsive forces. The force of repulsion
Frep =
/3 R
is caused by the cosmological constant and increases
with distance if
> 0. (For
negative this
becomes a force of `attraction', formally
resembling the force of confinement
between quarks which binds them within the nucleus.)
The opposite signs of the forces of attraction and repulsion in (5)
allow for a large number of new solutions
to the Einstein equations. As pointed out in the previous section,
Einstein himself used the repulsive effect of the cosmological constant to
balance the attraction of matter resulting in a static closed universe
which Einstein felt was in agreement with Mach's principle.
A quantitative analysis of solutions to (3) & (4) can
be gained by eliminating
in these
equations and combining them into a
single equation for the evolution of the scale factor in the presence of a
-term
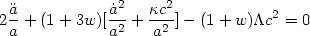
| (6) |
which is also valid if
is a function
of time (i.e. if Tik =
(t)
gik).
(We have assumed that matter has an equation of state
P = w
c2.)
A comprehensive quantitative analysis of (6) has been carried out in
[62] for a
cosmological constant, and in
[147]
for a time varying cosmological term
(t). For
our purpose it will be sufficient
to note that the qualitative behaviour of the universe
in the presence of a cosmological term which is
either constant or time varying,
can be understood very simply by rewriting
(3) in the suggestive form (we assume c = 1 for simplicity)
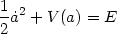
| (7) |
where
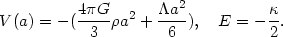
| (8) |
Since =
0(a0 / a)3(1 +
w), we find, substituting w = 0 for dust
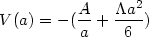
| (9) |
where A = 4G/3
0
a03.
(We assume for simplicity that matter is pressureless so that w =
0, however the qualitative analysis given below remains valid for matter
possessing more general equations of state.)
Equation (7) reminds one of classical motion with conserved
energy E in a one dimensional potential V(a) whose
generic form is shown in
Figure 2 for w = P /
0.
From the form of V(a) several things can be said about
the behaviour of the expansion factor a(t).
We shall first examine the case
= 1 (E < 0)
since it provides us with the
largest variety of qualitatively different solutions to the Einstein
equations.