


In 1917, only a few years after introducing the field equations of the General theory of relativity (GR), Einstein proposed adding a `cosmological constant' to these equations which were modified to
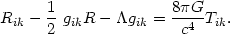
| (1) |
The main motivation behind introducing the cosmological constant appears to have been Einstein's belief that the equations of General Relativity should be compatible with Mach's principle. Einstein was fascinated by the arguments of philosopher/scientist Ernst Mach. Mach was concerned about the notion of absolute motion which prevailed in Newtonian mechanics. He postulated that all the matter in the universe including the distant stars provided a `background' against which motion could be measured and that unless there was a material background which served as a reference frame, it was meaningless to talk of rest or motion in any absolute sense (Mach 1893). Einstein proposed incorporating Mach's principle into the general theory of relativity by suggesting a solution of the equations (1) in which the universe was static and closed on itself, much like the closed two dimensional surface of a balloon. A static solution of (1) is possible to construct since, as shown in section 3, a positive cosmological constant introduces a repulsive force which can counterbalance the attractive force of gravity leading to the `static Einstein universe'. This universe has a finite spatial volume with no boundaries, furthermore the total mass in such a universe is related directly to its (finite) volume (section 3.1). A low mass universe has a small volume, and an empty universe has no volume at all ! The static Einstein universe thus incorporates Mach's principle since it demonstrates that without matter there can be no space against which background inertial effects can be measured.
It should be borne in mind that in 1917 the idea of the Milky Way being an island universe was widely believed in, and the notion of the existence of other galaxies had not yet been firmly established. All this was about to change however, when in the early 1920s Slipher's work showed that light from several spiral nebulae (later re-christened galaxies) was redshifted, a fact that could be explained by the Doppler effect if these nebulae/galaxies were moving away from us. (2) In 1922, about five years after Einstein had proposed his static solution, Aleksander Friedmann constructed a matter dominated expanding universe without a cosmological constant. The possibility that the universe may be expanding led Einstein to abandon the idea of a static universe and, along with it, the cosmological constant. In a 1923 letter to Weyl, Einstein is quoted as saying [150] "If there is no quasi-static world, then away with the cosmological term !" The conclusive discovery by Hubble (1929) of a linear expansion law relating redshift to distance made Friedmann models the standard geometrical framework within which Hubble's discoveries were subsequently interpreted [205, 213, 142, 154].
Introduced, then discarded, the cosmological constant
staged several comebacks, the first having to do with the realization that
the static Einstein universe was unstable and, if perturbed, could either
expand or contract. In 1927 Lemaitre constructed an expanding model which
originated from such an asymptotically static state in the distant past.
The Lemaitre model had a long age and has frequently been reinvoked
whenever the age constraints (associated with high values of
H0) get too tight for standard FRW models
(section 4.1). The Lemaitre model
was also discussed in the early 1960s
when observations appeared to show an excess of quasi-stellar objects
(QSO's) near the redshift
z  2. It was felt
that a universe which `hesitated' or `loitered'
near the quasi-static state at z ~ 2 for a sufficient amount of time
would naturally explain an
abundance of objects at that redshift.
Present arguments for a positive cosmological constant are
associated with observations of high redshift supernovae which indicate
2. It was felt
that a universe which `hesitated' or `loitered'
near the quasi-static state at z ~ 2 for a sufficient amount of time
would naturally explain an
abundance of objects at that redshift.
Present arguments for a positive cosmological constant are
associated with observations of high redshift supernovae which indicate

 =
=
 /
3H2 ~ 0.7,
and from cosmological simulations of structure formation which also
appear to favour a positive cosmological constant
[114,
144].
In the next section
we shall qualitatively analyze solutions of the Einstein equations with a
non-zero cosmological constant in a
Friedmann-Robertson-Walker (FRW) universe following the original path
taken by Eddington and Lemaitre.
/
3H2 ~ 0.7,
and from cosmological simulations of structure formation which also
appear to favour a positive cosmological constant
[114,
144].
In the next section
we shall qualitatively analyze solutions of the Einstein equations with a
non-zero cosmological constant in a
Friedmann-Robertson-Walker (FRW) universe following the original path
taken by Eddington and Lemaitre.
2 It is interesting that the same year that
Einstein introduced the cosmological term
 , de Sitter
presented solutions of (1) with Tik = 0,
, de Sitter
presented solutions of (1) with Tik = 0,
 > 0, which had
both static and dynamic features. Intriguingly,
although the space-time coordinatization originally introduced by de Sitter
was static
[43], namely
ds2 = cosh-2
Hr[dt2 - dr2 -
H-2 tanh2
Hr(d
> 0, which had
both static and dynamic features. Intriguingly,
although the space-time coordinatization originally introduced by de Sitter
was static
[43], namely
ds2 = cosh-2
Hr[dt2 - dr2 -
H-2 tanh2
Hr(d 2 + sin2
2 + sin2 d
d 2],
it allowed for a linear redshift-distance relation, since
2],
it allowed for a linear redshift-distance relation, since
 ttr
ttr
 0 in the above metric
resulting in the motion of test bodies by virtue of the geodesic equation
(d2 xi / d s2) +
0 in the above metric
resulting in the motion of test bodies by virtue of the geodesic equation
(d2 xi / d s2) +
 kli (dxk /
ds) (dxl / ds) = 0
(
kli (dxk /
ds) (dxl / ds) = 0
( kli is the affine connection).
This effect was pointed out by Weyl (1923)
and later used by Eddington to interpret Slipher's observations
in the context of de Sitter's static universe
[205].
Back.
kli is the affine connection).
This effect was pointed out by Weyl (1923)
and later used by Eddington to interpret Slipher's observations
in the context of de Sitter's static universe
[205].
Back.