4.1. H₀, q₀ and the Age of the Universe

The quest for understanding the geometry of our universe has been one of the central aims of cosmology since the 1960s and Alan Sandage in 1970 even described the whole of observational cosmology as being a "search for two numbers". The first of these numbers - the Hubble parameter H₀ = ( / a)₀, provides us with measure of the observable size of the universe and its age. The second q₀ = -H₀^-2( / a)₀ is called the deceleration parameter and probes the equation of state of matter and the cosmological density parameter. In the presence of a cosmological constant,

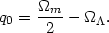
(13)

In a critical density universe with _m + = 1, the deceleration parameter

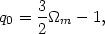
(14)

consequently a critical density universe will accelerate if _m < 2/3. The observational quest for q₀ showed that evolutionary effects play a dominant role in this important quantity and for a while it was felt that it may be virtually impossible to disentangle the true cosmological `signal' for q<sub>0</sub> from evolutionary `noise'. Recent years however have witnessed an important turnaround with the development of new and more powerful techniques which are either less sensitive to evolutionary effects or for which evolutionary effects are better understood.

In the next section, we shall consider several promising cosmological tests which could shed light on the composition of the universe and its geometrical properties. These tests include gravitational lensing, the use of high redshift supernovae as calibrated standard candles, and the angular size-redshift relation. Before we do that however, we shall turn our attention to another fundamental quantity which has traditionally played an important role in constraining cosmological models - the age-redshift relation.

The presence of a -term leads to an increase in the age of the universe with far-reaching observational consequences. To appreciate this let us first consider the critical density Einstein-de Sitter universe with a t^2/3, so that

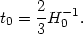
(14)

The value of H₀ therefore serves to determine the age uniquely in a spatially flat matter dominated universe. Moderately high values H₀ 75 km s^-1 Mpc^-1 result in an age for the universe which is smaller than the ages of the oldest globular clusters making an Einstein-de Sitter universe with a high value of H₀ difficult to reconcile with observations. The situation can be remedied if we live in an open universe. Assuming for simplicity that the universe is empty (a good approximation if _m 0.2) we get a t so that

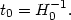
(16)

Combining (15) and (16) we get 2/3 H₀^-1 t₀ H₀^-1 for matter dominated cosmological models with _m 1. (A longer age t₀ > H₀^-1 can be achieved in the presence of a cosmological constant.) An open universe though older, nevertheless has two difficulties associated with it: the first is related to the growth of density perturbations which slow down considerably in an open universe leading to large primordial fluctuations in the Cosmic Microwave Background which may be difficult to reconcile with observations (assuming standard adiabatic fluctuations with scale-invariant initial spectra). The second is related to the Omega problem: a low Omega universe requires extreme fine tuning of initial conditions, which some find to be an unattractive feature of open/closed models.

Let us now consider a more general situation in which the universe has a -term in addition to normal matter. A closed form expression for the age of the universe in spatially flat models is given by [117]

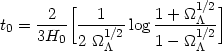
(17)

where = / 3H₀² = 1 - _m.

In Figure 3 we show the present age of a universe consisting of matter and a cosmological constant and parametrized in terms of the variables and _m. We find that the age of a flat universe with = 1 - _m is always greater than that of an open universe for identical values of 1 - _m. Additionally t₀ can exceed H₀^-1 if 0.74.

Figure 3. The age of the universe (in units of H0-1) is shown as a function of 1 - m for (i) flat models with a cosmological constant m + = 1 (solid line), and (ii) for open cosmological models m < 1 (dashed line).

No exact forms for t(H) are available for a time dependent -term. To study this and other cases, it is useful to express the Hubble parameter as a function of the cosmological redshift z. This can easily be done for a general multicomponent universe consisting of several non-interacting matter species characterized by equations of state P = w , for which the Hubble parameter can be written as

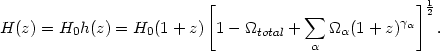
(18)

where _total = , = 1 + 3w and 1 + z = a₀ / a(t) is the cosmological redshift parameter.

Let us assume that the universe, in addition to matter and radiation, consists of a decaying -term modelled by a fluid with equation of state P_X = (m/3 - 1)_X so that = ₀(a₀/a)^m, m 2. The dimensionless Hubble parameter h(z) then becomes

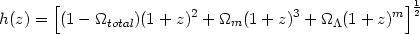
(19)

where m = 0 corresponds to a cosmological constant, and we neglect the presence of radiation. In a spatially flat universe _total = + _m = 1 (the present value of is therefore given by ₀ = 3H₀²[1 - _m]). A useful relationship between the cosmological time parameter t and the cosmological redshift z can be obtained by differentiating 1 + z = a₀ / a(t) with respect to time, so that dz / dt = - H(z)(1 + z). This leads to the following completely general expression for the age of the universe at a redshift z

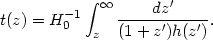
(20)

with h(z) supplied by either (18) or (19).

A running debate over the previous decade or so has centered around whether or not the universe has an `age problem', i.e. on whether matter dominated cosmological models are substantially younger than their oldest constituents (which happen to be metal poor old globular cluster stars). A key role in this controversy is played by the Hubble parameter, whose present value is known to within an uncertainty of about two. Higher values of H₀ clearly give rise to a younger universe whereas lower values lead to an older one.

At the time of writing lower values H₀ 65 km s^-1 Mpc^-1 are strongly supported by observations, especially in the light of new parallax measurements made by the Hipparcos satellite for Cepheid stars, which has led to a reanalysis of distances to globular clusters and consequently of their age estimates ⁽³⁾ which have dropped to 11.5 ± 1.5 Gyr [30, 120]. (Low values of H₀ are also suggested from an analysis of the Sunyaev-Zeldovich effect from X-ray emitting clusters [99], from Type 1a supernovae [165, 158] and from Cepheids observed by the HST.) Lower values of H₀ reconcile matter dominated flat models with the revised ages of globular clusters [120] and with limits from nucleochronology which indicate t₀ 7.8 Gyr [30]. Low values of H₀ combined with an absence of stellar systems with ages greatly exceeding 20 Gyr also argue against large values of , since from Fig 3 we see that 0.85 suggests an age t₀ 24 Gyr (if H₀ = 50km/sec/Mpc). Finally the recent supernovae based measurements of Perlmutter et al. (1998b) suggest a best-fit age of the universe t₀ 14.9 (63/H₀) Gyr for a spatially flat universe with _m 0.28 and 0.72.

The above arguments were largely limited to the present age of the universe. Ages of high redshift objects at z > 1 provide crucial information about the age of the universe at that redshift [110]. The existence of at least two high redshift galaxies having an evolved stellar population and hence an old age sets very severe constraints on a flat matter dominated universe [49, 119, 50, 152]. For instance the radio galaxy 53W091 at z = 1.55 discovered by Dunlop et al. (1996) is reported to be at least 3.5 Gyrs old. The age of a spatially flat matter dominated universe at a redshift z is easily obtained from (20) to be

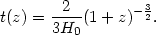
(21)

Consequently the discovery of 53W091 can be accommodated within an _m = 1, CDM model only if the Hubble parameter is uncomfortably small [119] H₀ 45 km s^-1 Mpc^-1. However both open and flat -dominated models alleviate the age problem for 53W091.

At even higher redshifts, recent work [212] aimed at age-dating a high redshift QSO at z = 3.62 using delayed iron enrichment by Type Ia supernovae as a cosmic clock, sets a lower bound of 1.3 Gyr on the age of the universe at that redshift. This discovery can be accommodated within a spatially flat cosmology only if _m + = 1 (low density open models with _m 0.2 are also permitted). However, the age dating of stellar populations requires complex modelling and although both open and flat -dominated models are clearly favoured by current observations, more work needs to be done before matter dominated flat models are excluded on the basis of age arguments alone. ⁽⁴⁾

³ An important indicator of the absolute age of a globular cluster star is its luminosity when it leaves the main sequence. Since luminosity is related to distance (to the star) ages of globular clusters are very sensitive to distance callibrators. Back.

⁴ It may be appropriate to mention that models with a cosmological constant may never be singular and therefore could possess an infinite age as demonstrated by the `bouncing models' in Fig. 1. However the value of the cosmological constant in such models is several orders of magnitude larger than permitted by current observations. The relevance of such models is therefore likely to be limited to the very early universe and will not affect the age problem discussed here. Back.