


4.2. The luminosity distance and gravitational lensing
Before proceeding to discuss possible constraints on

 from gravitational
lensing in this section and high redshift supernovae in the next,
let us introduce a quantity which plays a crucial role in these discussions,
namely the luminosity distance dL(z)
up to a given redshift z. Consider an object of absolute luminosity
from gravitational
lensing in this section and high redshift supernovae in the next,
let us introduce a quantity which plays a crucial role in these discussions,
namely the luminosity distance dL(z)
up to a given redshift z. Consider an object of absolute luminosity
 located at a coordinate
distance r from an observer at r = 0. Light emitted
by the object at a time t is received by the observer at t
= t0,
t and t0 being related by the cosmological
redshift 1 + z = a(t0) /
a(t). The luminosity flux reaching the observer is
located at a coordinate
distance r from an observer at r = 0. Light emitted
by the object at a time t is received by the observer at t
= t0,
t and t0 being related by the cosmological
redshift 1 + z = a(t0) /
a(t). The luminosity flux reaching the observer is

| (22) |
where dL is the luminosity distance to the object [142]

| (23) |
The luminosity distance dL depends sensitively upon both the spatial curvature and the expansion dynamics of the universe. To demonstrate this we determine dL using the expression for the coordinate distance r obtained by setting ds2 = 0 in (2), resulting in

| (24) |
which gives
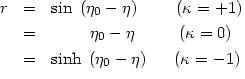
| (25) |
where  =
=
 0t
cdt / a(t).
0t
cdt / a(t).
Furthermore, since dz / dt = - (1 + z)H(z), we get

| (26) |
where h(z) = H(z) / H0 is defined in (18), and, in a universe with several components

| (27) |
Substituting (27) and (26) in (23) we get the following expression for the luminosity distance in a multicomponent universe with a cosmological term [26]

| (28) |
where

| (29) |
and S(x) is defined as follows:
S(x) = sin(x) if
 = 1
(
= 1
( total
> 1), S(x) = sinh(x) if
total
> 1), S(x) = sinh(x) if
 = - 1
(
= - 1
( total
< 1), S(x) = x if
total
< 1), S(x) = x if
 = 0
(
= 0
( total = 1).
total = 1).
Before we turn to applications, let us consider a simple
example which
provides us with an insight into the role played by the
luminosity distance dL in cosmology.
In a spatially flat universe the expression for dL
simplifies considerably,
so that we get for the matter dominated model (a
 t2/3):
t2/3):

| (30) |
On the other hand in de Sitter space (a
 exp(H0 t))
exp(H0 t))
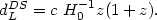
| (31) |
Comparing (30) and (31) we find
dLDS(z) >
dLMD(z),
which means that an object located
at a fixed redshift will appear brighter in
an Einstein-de Sitter universe than it will in de Sitter space
(equivalently in the steady state model).
(5)
This is also true for a
two component universe consisting of matter and a cosmological constant
as demonstrated in Fig 4. In a
spatially flat universe the presence of a
 -term increases the
luminosity distance to a given redshift, leading to interesting
astrophysical
consequences. Since the physical volume associated with a unit redshift
interval increases in models with
-term increases the
luminosity distance to a given redshift, leading to interesting
astrophysical
consequences. Since the physical volume associated with a unit redshift
interval increases in models with
 > 0, the
likelihood that light from a quasar
will encounter a lensing galaxy is larger in such models. Consequently
the probability that a quasar is lensed by
intervening galaxies increases appreciably in a
> 0, the
likelihood that light from a quasar
will encounter a lensing galaxy is larger in such models. Consequently
the probability that a quasar is lensed by
intervening galaxies increases appreciably in a
 dominated
universe, and can be used as a test to constrain the value of
dominated
universe, and can be used as a test to constrain the value of

 [72,
71,
192].
Following
[73,
26,
37]
we give below the probability of a quasar
at redshift zs being lensed relative to the fiducial
Einstein-de Sitter model
(
[72,
71,
192].
Following
[73,
26,
37]
we give below the probability of a quasar
at redshift zs being lensed relative to the fiducial
Einstein-de Sitter model
( m = 1)
m = 1)

| (32) |
where d (z1, z2) is a generalization of the angular distance dA = dL(1 + z)-2 discussed in Section 4.5:

| (33) |
where

| (34) |
and S( 12) is defined as follows,
S(
12) is defined as follows,
S( 12) =
sin(
12) =
sin( 12) if
12) if
 = 1
(
= 1
( total
> 1), S(
total
> 1), S( 12) =
sinh(
12) =
sinh( 12) if
12) if
 = -1
(
= -1
( total
< 1), S(
total
< 1), S( 12) =
12) =
 12
if
12
if  = 0
(
= 0
( total = 1).
In Fig 5 we show the lensing probability
P(lens) for the spatially flat universe
total = 1).
In Fig 5 we show the lensing probability
P(lens) for the spatially flat universe
 m +
m +

 = 1.
A large increase in the lensing probability over the fiducial
= 1.
A large increase in the lensing probability over the fiducial
 m = 1
value is clearly seen in models with low
m = 1
value is clearly seen in models with low
 m
(high
m
(high 
 ).
(For a broader analysis of parameter space see
[26].)
).
(For a broader analysis of parameter space see
[26].)
Turning now to the observational situation,
at the time of writing the best observational estimates give a
2 upper bound
upper bound

 < 0.66
obtained from multiple images of lensed quasars
[111,
112,
136].
Since radio sources are not plagued by some of the systematic
errors arising in an optical search (notably extinction in the lens
galaxy and the quasar discovery process) a search involving radio
selected lenses can yield useful complementary information to optical
searches [60].
Recent work by Falco et al (1998) gives
< 0.66
obtained from multiple images of lensed quasars
[111,
112,
136].
Since radio sources are not plagued by some of the systematic
errors arising in an optical search (notably extinction in the lens
galaxy and the quasar discovery process) a search involving radio
selected lenses can yield useful complementary information to optical
searches [60].
Recent work by Falco et al (1998) gives

 < 0.73 which
is only marginally consistent with optical estimates,
a combined analysis of optical and radio data yields a slightly more
conservative upper bound
< 0.73 which
is only marginally consistent with optical estimates,
a combined analysis of optical and radio data yields a slightly more
conservative upper bound

 < 0.62 at the
2
< 0.62 at the
2 level (for flat
universes)
[60].
(Constraints on
level (for flat
universes)
[60].
(Constraints on

 from both
lensing and Type 1a Supernovae are discussed in
[201];
also see next section. An interesting new method of constraining
from both
lensing and Type 1a Supernovae are discussed in
[201];
also see next section. An interesting new method of constraining

 from weak
lensing in clusters is discussed in
[67],
also see
[12]
and section 4.6.)
Improved understanding of statistical and systematic uncertainties combined
with new surveys and better quality data promise to make gravitational
lensing a powerful technique for constraining cosmological parameters and
cosmological world models.
from weak
lensing in clusters is discussed in
[67],
also see
[12]
and section 4.6.)
Improved understanding of statistical and systematic uncertainties combined
with new surveys and better quality data promise to make gravitational
lensing a powerful technique for constraining cosmological parameters and
cosmological world models.
5 For instance a galaxy at redshift z = 3 will appear 9 times brighter in a flat matter dominated universe than it will in de Sitter space (see Fig 4). Back.