4.4. Constraints on from the cosmic microwave background

On large angular scales 1° photons of the cosmic microwave background traveling to us from the last scattering surface probe scales that were causally unconnected at the time of recombination. ⁽⁸⁾ As a result observations of the CMB anisotropy on large scales provide us with a very clean probe of the primordial matter fluctuation spectrum before its distortion by astrophysical processes. On such large scales the main contribution to the CMB anisotropy comes from the Sachs-Wolfe effect

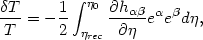
(39)

which relates temperature fluctuations to the integral of the variation of the metric evaluated along the line of sight [167]. The evaluation of (39) in a flat matter dominated universe is simplified by the fact that linearized the gravitational potential does not evolve with time, with the result that the above expression reduces to

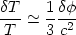
(40)

which relates fluctuations in the CMB to those in the gravitational potential at the surface of last scattering. Equation (40) can therefore be successfully used to determine the amplitude of primordial metric fluctuations with the help of COBE data. The presence of a cosmological constant however causes the linearized gravitational potential to evolve with time, the full Sachs-Wolfe integral (39) must therefore be used both to determine and normalize the primordial fluctuation spectrum [113].

The CMB temperature distribution can be written as

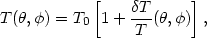
(41)

where T₀ is the blackbody temperature T₀ = 2.728 ± 0.004°K [65]. T / T can be written in terms of a multipole expansion on the celestial sphere:

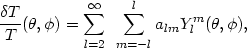
(42)

Information pertaining to a particular theoretical model is contained in the coefficients a_lm which are usually assumed to be statistically independent and distributed in the manner of a Gaussian random field with zero mean and variance

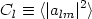
(43)

where the angle brackets indicate an ensemble average over possible universes.

The quantity that is directly measured by observations is the angular correlation of the temperature anisotropy

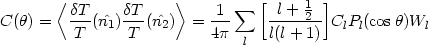
(44)

where cos = 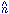₁ 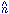^. ₂, P_l are Legendre polynomials and W_l is the filter function of the experiment used to measure the CMB; <> denote an ensemble average in the case of theoretical predictions and angular average in the context of observations. (The relationship between C() and the angular power spectrum C_l is analogous to that between the two point correlation function and the matter power spectrum P(k).)

At low multipoles l 60 the contribution to C_l is mainly from the Sachs-Wolfe effect due to scalar density perturbations and (in some models) tensorial gravity waves. (The value of the tenth multipole provides a convenient choice for normalization of the perturbation spectrum [22].) At large l > 60 however, the main contribution to C_l is due to oscillations in the photon-baryon plasma before decoupling, which leave their imprint in the CMB at the time of last scattering. These oscillations give rise to Doppler peaks in C_l the location of the peak being determined by the angle subtended by the sound horizon at the time of recombination (see figure 7). The sound horizon depends upon _baryon & _m whereas the angular diameter distance to the last scattering surface depends upon , _m and the spatial curvature of the universe. (Both and the spatial curvature are extremely small at the time of last scatter and therefore do not contribute to the sound horizon. On the other hand, the location of the doppler peak is not very sensitive to _baryon provided _baryon << _m + .)

Figure 7. The angular power spectrum of the cosmic microwave background is plotted against the angular wavenumber l (in radians-1). The predictions of the following theoretical models are tested against observations: (i) The flat CDM model with parameters (, m, b, h) = (0.7, 0.3, 0.05, 0.65) (dotted line); (ii) Flat CDM models with (m, b, h) = (1, 0.1, 0.5) and (m, b, h) = (1, 0.05, 0.5) (solid lines), the larger b model shows a higher Doppler peak; (iii) Open CDM model with (m, b, h) = (0.3, 0.05, 0.65) (broken line). Here m = cm + b, where cm is the cold (non-baryonic) matter component. For more details, see Peacock (1999) and Bond et al. (1997).

Since the angular scale corresponding to the first Doppler peak is sensitive to both the curvature of the universe and its matter content, its location can be used to place strong constraints on cosmological models. There are some indications that the first Doppler peak has been measured near l 260 Einstein is quoted as saying [86]. (The height of the peak is related to the baryon fraction in the universe and also to the scalar/tensor ratio S/T, the larger the baryon density the higher the peak, a small value of S/T reduces the peak height. The peak height also depends on the rate of expansion of the universe and hence on H₀ [97]; for low values _baryon 0.05 the peak height decreases if H₀ increases, whereas the reverse is true for a larger baryon fraction.) In figure 7 we show the angular power spectrum of the cosmic microwave background for the flat CDM model with = 0.7 (dotted line), for comparison we also show spatially flat (solid line) and open (dashed line) matter dominated models with _m = 1 and _m = 0.3 respectively.

It should however be pointed out that the CMB alone cannot uniquely differentiate between two models having identical matter content, perturbation spectra and with the same angular diameter distance to the last scattering surface. Such models will be degenerate in the sense that they will produce very similar CMB anisotropies [56, 57]. A degeneracy in parameter space happens to be a common feature of most cosmological tests. Fortunately different tests often have complementary degeneracies. (A degeneracy arises when a result remains unaffected by a specific combination of parameter changes.) For instance the degeneracy in the _m - plane from high redshift supernovae tests is almost orthogonal to that in a CMB analysis. Thus combining Type 1a supernovae measurements with the results from CMB experiments can serve to substantially decrease the errors on expected values of _m and as illustrated in figure 8 and figure 9 [209, 190, 56, 57]. Since the location of the Doppler peak near l 260 supports a spatially flat universe [86], a combined likelihood analysis of CMB anisotropy and Type 1a Supernovae data gives the best fit values [57]

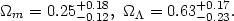
(45)

which strongly favour a flat universe with _m + 1 (also see [130, 191]).

Figure 8. The `cosmic complementarity' principle is beautifully illustrated by these best-fit contours obtained using expected data from future supernovae and CMB experiments. The 68% confidence regions are shown for three sets of hypothetical supernovae data likely to be recorded in five years time. The CMB analysis refers to the upcoming MAP and PLANCK satellite missions. The assumed fiducial model is CDM with m = 0.35, = 0.65 and H0 = 65 km. sec-1 Mpc-1. One clearly sees that the degeneracy in parameter space from supernovae observations is almost orthogonal to the degeneracy arising from CMB measurements. For more details see Tegmark et al. (1998).

Figure 9. Likelihood contours in the m - plane (left) are derived using a combined likelihood analysis of CMB and supernovae data. These contours show that the combined CMB+Sn likelihood function is strongly peaked at m = 0.25 and = 0.63 thereby favouring a flat universe (shown by the dotted-dashed straight line). The marginalized likelihood functions on the right are shown for SN data alone (dotted lines), CMB data alone (dashed lines) and the combined SN and CMB data (solid lines). The CMB+SN likelihood function sharply peaks near m + = 1. More details may be found in Efstathiou et al. (1998).

⁸ In matter dominated models the horizon at last scattering subtends an angle 1.8° _m^1/2(1000 / z_rec)^1/2 1.8° for _m 1 and z_rec 1000. In flat dominated models the dependence of on _m is much weaker, consequently 1.8° provides a good approximation for most values of _m. Back