4.3. Type 1a Supernovae and the value of

The luminosity distance also plays a crucial role in determining cosmological parameters once the absolute brightness of a class of objects is known. Of considerable importance in this context is the magnitude-redshift relation which relates the apparent magnitude m of an object to its absolute magnitude M

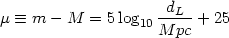
(35)

where µ is known as the distance modulus. Since d_L depends upon the geometry of space and its material content, the magnitude-redshift relation (35) can, in principle be used to determine and _total if both m and M are known within reasonable limits. ⁽⁶⁾

The recent discovery that type Ia supernovae may be used as calibrated standard candles for obtaining estimates of the luminosity distance d_L through (35) has aroused great interest. Type Ia supernovae are explosions which arise as a white dwarf star crosses the Chandrasekhar stability limit while accreting matter from a companion star [94, 4, 40]. The high absolute luminosity of SNe Ia (M_B - 19.5 mag) suggests that they can be seen out to large distances making them ideal candidates for measuring and constraining cosmological parameters [39, 21]. Of crucial import to using type Ia supernovae for estimating the luminosity distance d_L has been the observation that: (i) the dispersion in their luminosity at maximum light is extremely small ( 0.3 mag); (ii) the width of the supernova light curve is strongly correlated with its intrinsic luminosity: a brighter supernova will have a broader light curve indicative of a more gradual decline in its brightness [161]. Both (i) and (ii) reduce the scatter in the absolute luminosity of type 1a supernovae to ~ 10% making them excellent standard candles [21].

Nearby type 1a supernovae have been used to determine the value of H₀ whereas those further away are used to obtain reasonable estimates of cosmological parameters by minimizing the ² statistic

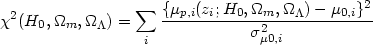
(36)

where µ_p are model dependent `predicted' values of the distance modulus obtained from (28) and (35), and µ₀(z_i) are the observed values. At least two groups - the Supernova Cosmology Project [157] and the High-Z Supernova Search Team [165] have been engaged in both finding and calibrating supernovae at low and high redshifts. At the time of writing, both groups have analyzed data for several dozen type Ia supernovae and a consensus seems to be emerging that a positive value of is strongly preferred. For instance, treating type 1a supernovae as standard candles and then using distance estimates to 42 moderately high redshift supernovae with z 0.83, Perlmutter et al. (1998b) find that the joint probability distribution of the parameters & _m is well approximated by the relationship (valid for _m 1.5)

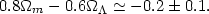
The best-fit confidence region in the _m - plane shown in (6) appears to favour a closed universe. However, as we shall see in the next section, when combined with the results of cosmic microwave experiments, the combined likelihood of _m, peaks near _m + 1.

Figure 6. Best-fit confidence regions in the m - plane obtained from the analysis of Type 1a high redshift supernovae of Perlmutter et al. (1998b). The upper-left shaded region corresponds to the singularity free `bouncing universe' models discussed in section 3.1.

These results provide an interesting insight into the expansion dynamics of the universe during its recent past. For instance, a cosmological model which passed through an epoch of matter domination before the present dominated epoch, also passed through an inflexion point at which the expansion of the universe changed from deceleration ( < 0) to acceleration ( > 0). From (3) & (4) it can be shown that this occurred at a redshift when was still not dominating the expansion dynamics of the universe. For instance from (4) we find that deceleration is succeeded by acceleration at the epoch

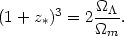
(37)

On the other hand the epoch of equality between _m and occurred at the redshift

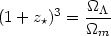
(38)

where = c² / 3H₀². Substituting the `best-fit' values obtained by Perlmutter et al. (1998b) for a flat universe _m 0.28, 0.72 we get z_* 0.726 and z_* 0.37 so that z_* < z _* . From (14)) we also get q₀ = - 0.58 for the deceleration parameter, indicating an accelerating universe (the combined Sn+CMB data give a slightly larger value q₀ - 0.5).

Supernovae data can also be used to constrain time dependent models of the kind discussed in section 8. In the case of scalar field models with potentials V() ~ ^-p and V() ~ (e^{1 /} - 1) the scalar field density in a spatially flat universe is constrained to lie in the range [159, 203] (0.6, 0.7) and the effective equation of state is w < - 0.6 (at the 95% confidence level).

A combined analysis of gravitational lensing and Type 1a supernovae gives the best-fit value _m 0.33 for a spatially flat universe [201]. Attempts to constrain the decay rate of a time-dependent cosmological term = ₀(1 + z)^m result in 0.24 _m 0.38 and m 0.85 (at the 68% confidence level) which in turn places constrains on the cosmic equation of state w = m/3 - 1 - 0.72. The combined supernovae & lensing data therefore convincingly rule out a network of tangled cosmic strings (w - 1/3) and strongly favour a cosmological constant (w = - 1).

The results obtained by both the Supernova Cosmology Project and the High-Z Supernova Search Team team present the strongest `direct' evidence for a non-zero cosmological constant. However much work needs to be done both in understanding systematic uncertainties as well as Sn Ia properties before the case for a positive is firmly established. ⁽⁷⁾ As we shall show in the next section, much stronger constraints on _m and emerge if we combine the supernovae results with observations of the cosmic microwave background.

⁶ In practice (35) must be corrected for effects associated with the redshifting of light as it travels to us, commonly called the K-correction. For instance photons being detected using a red filter would originally have had a `blue spectrum' if the source was located at z 1. Other possible sources of systematic errors include luminosity evolution, intergalactic extinction, Malmquist bias, the aperture correction, weak lensing etc. A more complete discussion of these issues can be found in [142, 154]. Back.

⁷ An accelerating universe can also be accommodated within the framework of the Quasi-Steady State Cosmology of Hoyle, Burbidge and Narlikar (1993). Back.