5. THEORETICAL ISSUES: VACUUM FLUCTUATIONS AND THE COSMOLOGICAL CONSTANT

Having summarised the observational evidence for a cosmological -term let us now turn our attention to some theoretical implicationsi of .

A turning point in our understanding of the cosmological constant occurred when Zeldovich (1968), intrigued by -based cosmological models presented to explain an excess of quasars near redshift ~ 2, showed that zero-point vacuum fluctuations must have a Lorentz invariant form P_vac = - _vac c², equivalently T_ik^vac = g_ik, i.e. the vacuum within the quantum framework had properties identical to those of a cosmological constant.

Let us review this situation beginning with an oscillator consisting of a single particle of mass m moving under the influence of a potential V = 1/2 kx². At the classical level one expects the lowest energy state to be associated with the particle at rest at x = 0, so that the total energy vanishes: E = T + V = 0. Thus, within the classical framework, the vacuum can be viewed as a state having zero energy and momentum. However when viewed in terms of quantum mechanics the situation changes, the uncertainty relation preventing the particle (wave function) from simultaneously having a fixed location (x = 0) and a fixed velocity (T = 0). As a result, the ground state energy of the oscillator is finite and is given by E = 1/2 , where = k/m. Turning now to quantum theory, it is well known that after secondary quantization a classical field can be looked upon as an ensemble of oscillators each with frequency (k). The net `zero-point energy' of this field is E = _k 1/2 (k). Thus the uncertainty relation endows the vacuum with both energy and pressure!

The existence of zero-point vacuum fluctuations has been spectacularly demonstrated by the Casimir effect. ⁽¹⁰⁾ The vacuum energy associated with zero-point fluctuations is formally infinite and results in a `cosmological constant problem' for the universe [205]. Because of the importance of this result we shall perform a simple calculation aimed at evaluating the zero-point energy associated with a quantized scalar field in flat space-time. (The reader is referred to Birrell & Davies 1982 for a discussion of quantization of higher spin fields.)

Consider the action defined in flat four dimensional space-time ⁽¹¹⁾

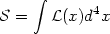
(53)

where (x) is the Lagrangian density for a massive scalar field

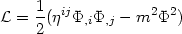
(54)

propagating in flat space-time with metric _ij.

The variational principle = 0 gives the Klein-Gordon equation

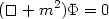
(55)

where ^ik _{i k}.

To quantize the system we treat the field as an operator

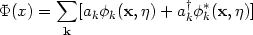
(56)

where a_k, a_k^† are annihilation and creation operators [a_k, a_k'^†] = _kk', defining the vacuum state a_k| 0> = 0, 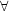k. An orthonormal set of solutions defined using periodic boundary conditions on a three dimensional torus of side L is given by [18]

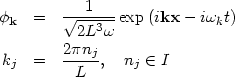
(57)

where _k² = k² + m², and the field modes have been normalized using

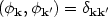
(58)

where

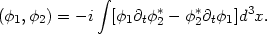
(59)

Consider next, the energy-momentum tensor

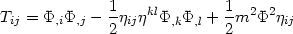
(60)

where T₀₀ defines the energy density

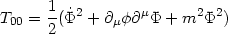
(61)

and T₀ the momentum density

(62)

Substituting from (56) & (57) into (60) one obtains for the Hamiltonian H

(63)

which can be further simplified using the commutation relation [a_k, a_k'^†] = _kk' to

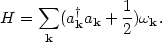
(64)

A similar operation on the momentum density yields [18]

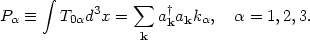
(65)

Inspecting expressions (63) and (65) for the Hamiltonian H and the momentum operator P we find, for the expectation value of these quantities in the vacuum state |0>

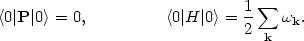
(66)

Transforming the sum _k to an integral we get

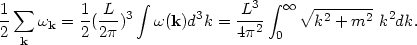
(67)

From (66) & (67) we find that the energy density of zero-point vacuum fluctuations is dominated by ultraviolet divergences which diverge as k⁴ when k . The vacuum state therefore has zero momentum and infinite energy ! (In terms of Feynman diagrams the energy density of zero-point fluctuations is associated with a one-loop vacuum graph, see figure (13).)

Within the framework of Newtonian gravity and either classical or quantum mechanics, an infinite (or very large) vacuum energy does not cause serious problems since interaction between particles is governed not by the absolute value of the potential energy V, but by its gradient V. As a result one can always redefine V' V + V₀ so that the minimum of V' has zero net energy. The situation changes dramatically when we view the vacuum within the framework of general relativity. A central tenet of the general theory of relativity is that the gravitational force couples to all forms of energy through the Einstein equations G_ik = (8G / c⁴)T_ik. Therefore if the vacuum has energy then it also gravitates ! In order to probe this effect further one needs to know the equation of state possessed by the vacuum energy, equivalently the form of its energy momentum tensor T^ik_vac. This question was answered by Zeldovich (1968) who showed that the vacuum state had to have a Lorentz-invariant form, one that was left unchanged by a velocity transformation and hence appeared the same to all observers. This requirement is exactly satisfied by the equation of state P = - possessed by the cosmological constant, since the relation T_ik = g_ik is manifestly Lorentz-invariant. ⁽¹²⁾

All fields occurring in nature contribute an energy density to the vacuum and expressions analogous to (66) for bosons can also be derived for fermions. Since fermionic creation, annihilation operators anti-commute this leads to

(68)

Comparing (68) with (66) we find that the zero-point energy of fermions is equal and opposite to that of bosons (having identical mass).

The advent of Supersymmetry in the 1980s, incorporating a fundamental symmetry between bosons and fermions, led to the hope that the cosmological constant problem would finally be resolved, since the one-to-one correspondence between bosons and fermions in such theories was expected to lead to cancellation between bosonic and fermionic infinities [216]. However Supersymmetry is expected to exist only at very high energies/temperatures. At low temperatures such as those existing in the universe today, Supersymmetry is broken. One might therefore expect the cosmological constant to vanish in the early universe only to reappear later, when the universe has cooled sufficiently so that T << T_SUSY > 10³ GeV. Thus the cosmological constant problem re-emerges to haunt the present epoch !

Although the cosmological constant problem remains unresolved, an important aspect of Zeldovich's work was that it demonstrated a firm physical mechanism for the generation of a cosmological constant. Later work, mostly associated with Inflationary model-building, further strengthened this idea by showing that an effective cosmological constant could arise due to diverse physical processes including symmetry breaking, vacuum polarization in curved space-time, higher dimensional `Kaluza-Klein' theories etc. Some of these developments have been reviewed in Einstein is quoted as saying [132].

¹⁰ The Casimir effect arises because vacuum fluctuations satisfy the quantum mechanical wave equation and hence are sensitive to boundary conditions. As shown by Casimir (1948) the presence of two flat parallel conducting plates at a separation l, alters the distribution of electromagnetic field modes existing in the vacuum, resulting in an attractive force per unit area between the plates: F = - c ² / 240l⁴ which is of vacuum origin. The Casimir effect has been experimentally measured by Spaarnay (1957) and others Einstein is quoted as saying [18, 189, 205, 139]. Back.

¹¹ Following Landau & Lifshitz (1975) we use Latin indices to describe space-time coordinates, so that i,j,k... = 0,1,2,3; and Greek indices to describe spatial coordinates: , , .. = 1,2,3. Back.

¹² Zero-point fluctuations are usually regularized by `normal ordering' - a rather ad hoc procedure which involves the substitution a<sub>k</sub> a<sub>k</sub><sup>†</sup> a<sub>k</sub><sup>†</sup> a<sub>k</sub> in [63]. In curved space-time a single regularization is not enough to rid <T<sub>ik</sub>> of all its divergences. Three remaining `infinities' must be regularized, leading to the renormalization of additional terms in the one-loop effective Lagrangian for the gravitational field, which, in an FRW universe becomes: _eff = -g [ + R / 16 G + R² + R_ij R^ij]. Renormalization of the first term 0 corresponds to normal ordering. The presence of the second term R / 16 G, led Sakharo v to postulate that the gravitational field might be `induced' by one-loop quantum effects in a curved background geometry, since one could recover the ordinary Einstein action by renormalizing the `bare' value G to its observed value: G G_obs [173]. Thus both the cosmological constant and the gravitational constant G may be induced by quantum effects. The remaining two terms in _eff give rise to vacuum polarization effects and have been extensively discussed in the literature [18, 81]. Back.