6. THE COSMOLOGICAL CONSTANT AND SPONTANEOUS SYMMETRY BREAKING

An important development in our understanding of the `vacuum energy' was associated with the phenomenon of symmetry breaking in the electroweak Weinberg-Salam model. Consider the scalar field action

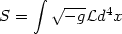
(69)

where is the Lagrangian density

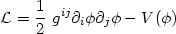
(70)

and the scalar field potential has the form

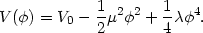
(71)

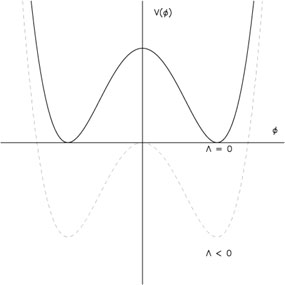
This particular form of the potential (illustrated in Fig. 12) endows the system with some interesting properties. For instance since the symmetric state = 0 is unstable (V''() < 0) the system settles in the ground state = + or = -, where = [µ² / ]^1/2 thus breaking the reflection symmetry - present in the Lagrangian. The energy momentum tensor T_ik of a scalar field with Lagrangian density is given by

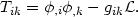
(72)

Assuming to be homogeneous and time-independent one finds the ground state energy-momentum tensor to be

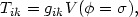
(73)

the vacuum state therefore has precisely the form of an effective cosmological constant T_ik = g_{ik eff} where _eff = V( = ) = V₀ - µ⁴ / 4. Setting V₀ = 0, results in a negative cosmological term _eff = -µ⁴ / 4. Substituting parameters arising in the electroweak theory results in a lower limit on the value of the vacuum energy density [205] _vac = |_eff| / 8 G = 10⁶ GeV⁴, which is almost 10⁵³ times larger than current observational upper limits on the cosmological constant _vac,0 = ₀ / 8 G ~ 10^-29 g/cm³ 10^-47 GeV⁴. Clearly in order not to violate observational bounds today, one must set V₀ µ⁴ / 4 so that _eff ~ ₀. An interesting feature of this `regularization' of the cosmological constant is that, while drastically reducing the value of the cosmological constant today it simultaneously generates a large cosmological constant ~ V<sub>0</sub> during an early epoch before symmetry breaking, thereby giving rise to the possibility of Inflation ! The cosmological constant problem therefore presents us with a dilemma: it is certainly good to have a large cosmological constant during an early epoch so as to resolve - via Inflation - the horizon and flatness problems and possibly generate seed fluctuations for galaxy formation. However one must simultaneously ensure that the value of today is small so as not to conflict with observations. As we have seen, in models with SSB this dual requirement of `large in the past + small at present' results in an enormous fine tuning of initial conditions.

Figure 12. The `Mexican top-hat' potential describing spontaneous symmetry breaking shown: before (dashed) and after (solid) the cosmological constant has been `renormalized'.