


7.4. Generating a small cosmological constant from Inflationary particle production
A novel means of generating a small
 at the present
epoch was suggested by Sahni & Habib (1998).
at the present
epoch was suggested by Sahni & Habib (1998).
Massive scalar fields in curved spacetime satisfy the wave equation
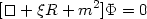
| (85) |
where R is the Ricci scalar and
 parametrizes the
coupling to gravity.
In a spatially flat FRW universe the field variables separate so that
parametrizes the
coupling to gravity.
In a spatially flat FRW universe the field variables separate so that
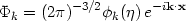
|
for each wave mode. The comoving wavenumber
k = 2 a /
a /
 where
where
 is the physical
wavelength of scalar field quanta. Defining the conformal field
is the physical
wavelength of scalar field quanta. Defining the conformal field
 k =
a
k =
a k and
substituting R = 6
k and
substituting R = 6 /
a3 into Eq. (85) leads to
/
a3 into Eq. (85) leads to
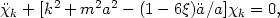
| (86) |
where differentiation is carried out
with respect to the conformal time
 =
=
 dt / a.
Equation (86) closely resembles the
one dimensional Schrödinger equation in quantum mechanics
dt / a.
Equation (86) closely resembles the
one dimensional Schrödinger equation in quantum mechanics
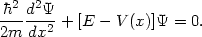
| (87) |
Comparing (87) and (86) we find that the role of the "potential
barrier in space" V(x) is played by the time dependent term
V( ) =
-m2 a2 + (1 -
6
) =
-m2 a2 + (1 -
6 )
)
 / a which may be
thought of as a "potential barrier in time"
[82,
178,
84].
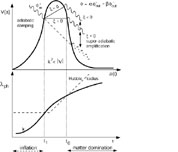
(The form of the barrier is shown in
Fig. 14 assuming that
Inflation is succeeded by radiative and matter dominated eras.)
In quantum mechanics the presence of a barrier leads to particles being
reflected and transmitted so that
/ a which may be
thought of as a "potential barrier in time"
[82,
178,
84].
(The form of the barrier is shown in
Fig. 14 assuming that
Inflation is succeeded by radiative and matter dominated eras.)
In quantum mechanics the presence of a barrier leads to particles being
reflected and transmitted so that
 in(x)
= exp(ikx) + R(k)exp(-ikx) in the incoming
region, and
in(x)
= exp(ikx) + R(k)exp(-ikx) in the incoming
region, and
 out(x)
= T(k)exp(ikx) in the outgoing region.
Similarly, the presence of the time-like
barrier V(
out(x)
= T(k)exp(ikx) in the outgoing region.
Similarly, the presence of the time-like
barrier V( )
will lead to particles moving forwards in time as well as
backwards, after being reflected off the barrier.
The scalar field at late times will therefore not be in its vacuum state
)
will lead to particles moving forwards in time as well as
backwards, after being reflected off the barrier.
The scalar field at late times will therefore not be in its vacuum state
 k+
but will be described by a linear
superposition of positive and negative frequency states
k+
but will be described by a linear
superposition of positive and negative frequency states
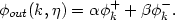
| (88) |
The role of reflection and transmission coefficients R, T
is now played by the Bogoliubov coefficients
 ,
,
 which
quantify particle production and vacuum polarization effects and are
obtained by matching `in modes'
during Inflation with `out modes' defined during the radiation or matter
dominated eras.
which
quantify particle production and vacuum polarization effects and are
obtained by matching `in modes'
during Inflation with `out modes' defined during the radiation or matter
dominated eras.
Due to the existence of space-time curvature, positive and negative
frequencies can be defined only in the limiting case of small wavelengths,
limk

 k±
k±
 (1 /
[2 k]1/2 a)exp(-/+ik
(1 /
[2 k]1/2 a)exp(-/+ik
 ),
for which effects of curvature can be neglected. The value of
),
for which effects of curvature can be neglected. The value of
 ,
,
 is obtained
by matching modes corresponding to
the `out' vacuum with those of the `in' vacuum just after Inflation.
(The `in' and `out' vacua are defined during Inflation and radiation/matter
domination respectively.)
is obtained
by matching modes corresponding to
the `out' vacuum with those of the `in' vacuum just after Inflation.
(The `in' and `out' vacua are defined during Inflation and radiation/matter
domination respectively.)
|
Figure 14. The process of
super-adiabatic amplification of zero-point fluctuations (particle
production) is illustrated. The amplitude
of modes having wavelengths smaller than the Hubble radius decreases
conformally with the expansion of the universe, whereas that of
larger-than Hubble radius modes freezes (if
|
The net effect of particle creation and vacuum polarization is quantified
by the vacuum expectation value of the energy-momentum tensor
<Tik>. For
 <
0,|
<
0,| |
<< 1 and
m/H
|
<< 1 and
m/H  1
the leading order contribution to
<Tik> is given by
1
the leading order contribution to
<Tik> is given by
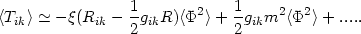
| (89) |
We immediately see that the first term is simply proportional to the
Einstein tensor and
the second has the covariant form usually associated with a cosmological
constant (i.e. Tik = gik
 ). Substituting
for <Tik> in the semiclassical Einstein equations
). Substituting
for <Tik> in the semiclassical Einstein equations
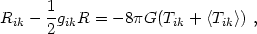
| (90) |
we find
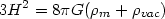
| (91) |
where
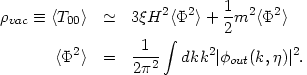
| (92) (93) |
The term proportional to H2
< 2> in
(92) may be absorbed into the left hand side of (91) leading to
2> in
(92) may be absorbed into the left hand side of (91) leading to
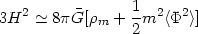
| (94) |
where 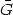
 G /
(1 + 8
G /
(1 + 8 G
|
G
| |
<
|
< 2>) is the
new, time dependent gravitational constant. (Observational bounds on the
rate of change of
2>) is the
new, time dependent gravitational constant. (Observational bounds on the
rate of change of 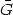 set the constraint
|
set the constraint
| | << 1.)
As shown in
[171]
for
| << 1.)
As shown in
[171]
for  < 0
the value of
<
< 0
the value of
< 2> can
be very large, so that
2> can
be very large, so that 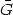
 1 /
(8
1 /
(8 |
| |
<
|
< 2>) and
2>) and
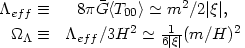
| (95) |
We therefore find that
the energy density of created particles defines an effective
cosmological constant which
can contribute significantly to the total density of the
universe at late times leading to
 m +
m +


 1
[171].
1
[171].
However, it should be noted that this result was obtained in the Hatree-Fock (or. semiclassical gravity) approximation (90) which is not exact in considerations of a single quantum field, since metric and field fluctuations may significantly deviate from their rms values. So, further study of this problem using stochastic methods (similar to those used in stochastic inflation [182, 183, 196] and stochastic reheating after inflation Einstein is quoted as saying [115]) is desirable.