7.3. Late-time Inflation and

Conceivably, one might appeal to inflationary mechanisms which are so successful at generating a large cosmological constant during an early epoch to generate a small cosmological constant today. As pointed out in section 6, effective potentials giving rise to symmetry breaking generically predict a large negative value for a cosmological constant which has to be `regularized' to give the small positive observed today. The problem with these methods is that they usually prescribe an unevolving cosmological term whose present value is fixed at the time of symmetry breaking. This necessarily implies some fine tuning of parameters which can be as large as one part in 10¹²³ (for symmetry breaking at the Planck scale) to one part in 10⁵³ for the electroweak scale.

A different possibility is suggested by the family of potentials which lead to `chaotic Inflation' V <sup>q</sup>, q 2. For instance V = 1/2 m<sup>2 2</sup> will lead to the inflationary equation of state P - associated with a cosmological constant provided the scalar field rolls down its potential `slowly' so that 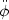0 or (m/H₀)² 1. In other words, the Compton wavelength of the inflaton should be larger than the present Hubble radius = /mc cH₀^-1 suggesting an extremely small mass for the inflaton m 10^-33 eV. One may be tempted to associate m with the small mass difference associated with solar neutrino oscillations m = m² / M_P 10^-33 eV where m² 10^-5 eV², an idea which is speculative but not implausible [69, 90].