8.3. Relation between kinematic and dynamical descriptions of

As pointed out in the previous section, although kinematic and dynamical models of lie on completely different levels of fundamentality from the theoretical point of view, they may be equivalent if a background space-time is described by a FRW model. In particular, the simplest class of kinematic models

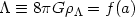
(111)

is then equivalent to hydrodynamic models based on an ideal fluid with the equation of state

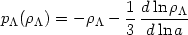
(112)

(with a being excluded from Eq. (112) using Eq. (111)).

Let us go further and present the correspondence between a popular subclass of these models where a^- (or, equivalently,

p = ( / 3 - 1) ) and field-theoretical models for a minimally coupled lambda-field following [187] where the particular case = 2 (i.e. the -term mimicking temporal behaviour of spatial curvature or non-relativistic cosmic strings) was considered. This gives an explicit example of the reconstruction of a lambda-field potential from H(a). Now = 0 is assumed for simplicity, and we take 0 < 3. The left inequality is necessary for the condition (99) to be satisfied, while the right inequality guarantees that << _m during the matter-dominated stage while z >> 1 (in addition, this condition makes p negative). In this case, the Hubble parameter H(a) is given by

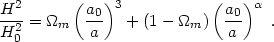
(113)

Using the 0 - 0 background Einstein equation and Eq. (98), the lambda-field potential V() can be expressed in terms of H(a):

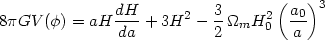
(114)

which reduces to

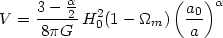
(115)

for the case under consideration.

Now Eq. (98) may be integrated for the given H(a) dependence to obtain

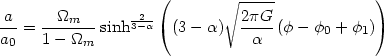
(116)

where ₀ is the present value of the lambda-field and

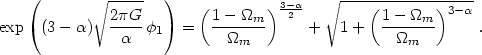
(117)

Finally, combining Eqs. (115, 116) we get an explicit expression for the interaction potential:

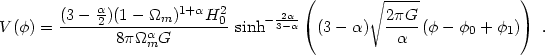
(118)

At early times during the matter-dominated stage, this potential is an inverse power-law (V() ( - ₀ + ₁)^{- 2 / (3 - )}) (we do not consider here what happens with V() even earlier, during the radiation-dominated stage). While during the current, -dominated epoch, it changes its form to an exponential. This shows why the assumptions of a purely power-law dependence of on a or, equivalently, of a linear equation of state p = w , w = const are not "natural": they require fine-tuning between the present value of the lambda-field ₀ and the value of where the potential changes its form. On the other hand, neither can this possibility be ruled out completely.

In addition, this example of reconstruction of V() shows that, in field-theoretic models of based on a minimally coupled scalar field, there is no lower limit on the present value of w other than -1 (which follows from the weak energy condition (99)). The opposite statement in [215, 188] is a consequence of a number of additional assumptions (equipartition of energy densities of all fields including the lambda-field at the end of inflation, use of a subclass of possible initial contitions whose solutions for have reached an intermediate asymptote which they call the "tracker" solution by the present time, consideration of some special classes of potentials), none of which is obligatory. In particular, a "tracker" solution may have w arbitrarily close to -1 at present, if an inverse power-law potential with a small exponent is used.