8.4. Reconstructing the effective potential V() for a time-dependent -term

In view of the large number of models capable of predicting a small cosmological constant at the present epoch, it is necessary to ask whether cosmological observations themselves may be used to determine model parameters uniquely. The answer to this question is (fortunately) in the affirmative, at least for the class of minimally coupled scalar field models discussed earlier. This is easily demonstrated by considering Equations (114) and (98) which express V() and in terms of the Hubble parameter H and its first derivative dH/dz. Consequently one can determine the form of the potential V(z) (mimicking the -term) if the Hubble parameter H(z) is known from observations. There are two independent methods for determining H(z). The first is related to the luminosity distance d_L, discussed in section 4.2 [186, 101]. From (28) we easily find

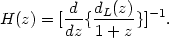
(119)

Thus the luminosity distance d_L(z) determines the Hubble parameter H(z) uniquely ! Now (98, 114) can be used to reconstruct the form of the potential V(z) (or V()) and the equation of state w(z) in a model independent manner. (However, what is required for an unambiguous determination of V() is the present matter density _m [186].) Formula (119) can also be used for an unambiguous determination of H(z) from the angular-size distance d_A(z) introduced in section 4.5, if we use the relation d_A(z) = d_L(1 + z)^-2 [187].

Another means of determining H(z) is associated with the growth of linear density fluctuations responsible for the formation of large scale structure [185, 186]. The growth of linearized perturbations in a collisionless medium has the well known form

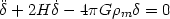
(120)

where the value of H is determined from (97). (On scales << 200h^-1 Mpc the -field is practically unclustered and can be treated as a smooth component if |m²| |d²V / d²| img src="../../New_Gifs/ltapprox.gif" alt="ltapprox"> H₀²). Although it is not possible to solve (120) analytically for an arbitrary potential V(), the inverse problem of determining H once is known is exactly solvable ! We demonstrate this by first performing a change of variables t a, d / dt aHd / da which reduces (120) to a first order linear differential equation for H²:

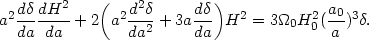
(121)

Equation (121) has the exact solution

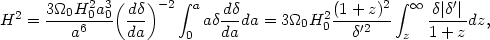
(122)

where ' = d / dz. Setting z = 0 in this expression, we arrive at a very interesting relationship between ₀ and (z):

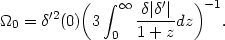
(123)

Substituting this relationship in (122) we finally obtain

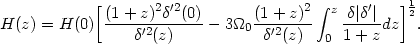
(124)

Clearly knowing and ' we can determine H(z) and hence V(z). For very large z, z >> 1, observational difficulties make it unlikely that will be known to great accuracy, at least in the near future. However in this regime the flat matter dominated solution (1 + z)^-1 provides a very good approximation since _m 1 for z >> 1.

It should be pointed out that the above method of reconstructing the -term potential from observations is complementary to that used to reconstruct the inflaton potential [126]. Whereas the luminosity distance d_L or the growth rate of the linearized density contrast (z) can be used to reconstruct V(), the inflaton potential is reconstructed on the basis of the primordial amplitude and spectrum of relic density perturbations and gravity waves created during inflation (also see [141]).