AND ANTHROPIC
ARGUMENTS FOR ITS SMALL VALUE
In this, the final section of our review, we must ask
the following question: do we expect the present value of
to be
fundamental (= defined by the parameters of a physical theory)
or accidental (= determined by initial conditions in the
early Universe)? At present, we have no answer to this question. Models for
considered in
previous sections admit both possibilities.
For instance, in the class of minimally-coupled lambda-field models
with an inverse power-law potential, the present value of
is fundamental
(= defined by the parameters of
V(
) only) if
"initially" (at the end
of inflation or at a later moment when the lambda-field becomes a separate
degree of freedom of matter)
was sufficiently small, so that the corresponding solution for
(t) had time to reach
a future attractor (the "tracker" solution of
[215,
188])
by the present epoch.
On the other hand, if the initial value
in is large,
then the present value
0
in, and the current
value of the
-term
is accidental. Note that in the latter case
is practically time
independent now. Such a large value of
in may, for
instance, be generated during an early inflationary stage, in which case
stochastic methods
[182,
183,
196]
may be used to derive probability distributions for
in and
. As a byproduct
of such a mechanism, small quasi-static inhomogeneous perturbations of
will also be
generated.
(15)
If is accidental,
then a wide range of "explanations" for its currently
(small) value can be given, based on
the most reliable form of the anthropic principle - the
weak anthropic principle. However, even if
is fundamental
and can be
expressed through other microphysical constants, one may still try to use
a more controversial form of this principle - the strong anthropic
principle.
(16)
An anthropic argument for
> 0 has been
suggested by Banks (1985) and
Weinberg (1987),
who felt that the extraordinary difference between likely values of the
vacuum energy
~
m
~ 10-29 g/cm3
and the expected value (from a consideration of Planck scale physics)
P ~
1093 g/cm3 could
only be understood through anthropic arguments, since, in the absence of a
fundamental symmetry which set the value of
to precisely zero,
it would be extremely fortuitous if particle physics determined a value for
which was comparable to the matter density at this precise
moment in the history of the universe. The case for the anthropic principle
as a viable means for understanding properties of
the universe has received a strong measure of
support from recent developments in inflationary cosmology.
A self-consistent treatment of quantum effects in inflationary models
has shown that the entire universe may consist of an ensemble
of sub-universes (separated from each other by particle horizons) having
`all possible types of vacuum states and all possible types of
compactification' of extra space-time dimensions
[131].
According to this picture
our observable universe is but one of an infinite
number of universes each having its own set of conserved quantities and
dimensions.
Since in each sub-universe physical fields determining the value of
have distinct values it is reasonable to expect that the value of
varies from one
sub-universe to another.
Weinberg (1987) showed that large values of
were unlikely to be
`observed' since the presence of observers demanded the existence of
galaxies
and galaxy formation was strongly suppressed if the energy in the
cosmological constant greatly exceeded the matter density (also see
[55,
198]).
Martel, Shapiro & Weinberg (1998) have suggested that the
probability that observers living in a given sub-universe will measure
a value
for the `vacuum
energy' be given by the expression
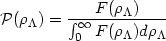
| (125) |
where F() is the fraction of matter in galaxies in a
sub-universe with vacuum energy
=
/
8
G
[137].
The value of F() is
calculated assuming Gaussian initial fluctuations at recombination,
with a COBE-normalized
cold dark matter spectrum with a cosmological
constant (CDM).
The requirement that the observed value
, * in
our sub-universe equal
the statistical mean or median evaluated over
all sub-universes (i.e.
, * =
<>, where
=
/
3H02) gives
a value which peaks in the region
, * ~
0.6 - 0.9 for a broad region of parameter space and
assuming fairly reasonable conditions for galaxy formation
[137].
Thus small observed values of
appear to be
strongly disfavoured by the anthropic argument !
15 Previous discussions involving quantum
cosmology also held the possibility that the value of
is not determined
uniquely. For instance Hawking (1984)
showed that the wave function for the universe could contain a
superposition of terms with different values for the cosmological
constant.
Investigating the effect of wormholes on quantum gravity, Coleman
(1988a,b)
subsequently showed that coupling constants whose values were not fixed
by symmetries in the Lagrangian could take on all possible values in
the superposition of terms describing the state vector in quantum cosmology.
Back.
16 The weak anthropic principle in the narrow sense states that our location in space and time should be such that it admits the existence of intelligent life. An extension of this principle is that initial conditions allow the existence of such a region in space-time. On the other hand the strong anthropic principle states that laws of nature should permit the existence of intelligent life. It may be noted that the border between these two versions of the anthropic principle is not absolutely rigid. Namely, by generalizing a physical theory (say, the electroweak model) with fixed constants into a more general theory where these constants may have arbitrary values depending upon initial conditions, we make a step from the strong to the weak anthropic principle (also see [11]). Back.