2.6. Velocity distribution of galaxies

The existence of the morphological sequence of clusters from irregular to regular clusters (Section 2.5) suggests that the regular clusters may have undergone some sort of dynamical relaxation. The nature of this relaxed distribution is examined in the next two sections through the distribution of cluster galaxy velocities and positions.

The redshifts in Section 2.2 are determined from the mean radial velocity of galaxies in a cluster; in fact, the radial velocities of individual galaxies are distributed around this mean. It has been conventional to characterize this distribution by the dispersion _r of radial velocities about the mean

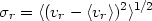
(2.4)

where v_r is the radial velocity, which is the component of the galaxy velocity along the line-of-sight. The dispersion completely characterizes the radial velocity distribution function if it is Gaussian:

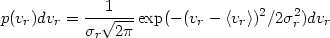
(2.5)

Here, p(v_r)dv_r is the probability that an individual cluster galaxy has a radial velocity in the range v_r to v_r + dv_r. While the Gaussian distribution has usually been adopted simply for convenience, statistical tests reveal that it is a consistent fit to the observed total distribution function in many clusters, at least if high velocities (|v_r - <v_r>| > 3_r) are excluded (Yahil and Vidal, 1977). However, the velocity dispersion in a given cluster generally decreases with distance from the cluster center; in Coma and Perseus the decline is about a factor of two from the center to the outer edge (Rood et al., 1972; Kent and Gunn, 1982; Kent and Sargent, 1983). Moreover, the velocity dispersion can differ in different clumps of an irregular cluster showing subclustering (Geller and Beers, 1982; Bothun et al., 1983).

A Gaussian distribution for a single component of the velocity obtains for a system of non-identical particles in thermodynamic equilibrium, in which case we identify the velocity dispersion with _r (kT/m)^1/2, where T is the galaxy 'temperature' and m the galaxy mass. While the Gaussian velocity distribution found in clusters suggests that they are at least partially relaxed systems, they are not fully relaxed to thermodynamic equilibrium. In thermodynamic equilibrium, all components of the cluster would have equal temperatures; what is observed is that it is the velocity dispersion (not temperature) which is nearly independent of galaxy mass and position (Rood et al., 1972; Kent and Gunn, 1982; Kent and Sargent, 1983).

Some variation of the velocity dispersion with galaxy mass or cluster position is observed (Rood et al., 1972; Kent and Gunn, 1982; Kent and Sargent, 1983). In the Coma and Perseus clusters, the most luminous galaxies have a somewhat smaller velocity dispersion than the less luminous galaxies, and the velocity dispersion decreases with increasing projected distance from the cluster center. In fact, the latter effect must necessarily occur if clusters are finite, bound systems. Then, the velocities of bound galaxies at any point in the cluster cannot exceed the escape velocity at that position. As the escape velocity decreases with increasing distance from the cluster center, the velocity dispersion must also decrease with projected distance from the cluster center.

The observed mean galaxy velocity <v_r> will depend on the projected position in the cluster if the cluster is rotating. The projected shapes of many clusters are substantially flattened. Of course, this is true of the L (line) and F (flat) clusters (Section 2.5); however, many regular (cD and B) clusters are also significantly flattened (Abell, 1965; Dressler, 1981). If these clusters are actually oblate in shape due to significant rotational support, the variation in <v_r> across the cluster would be expected to be comparable to _r. In fact, such large velocity gradients are not observed (Rood et al., 1972; Gregory and Tifft 1976; Schipper and King, 1978; Dressler, 1981); apparently, the flattening of clusters is not due to rotation.

Useful compilations of velocity dispersions for clusters have been given by Hintzen and Scott (1979), Danese et al. (1980), and particularly Noonan (1981).