1.1. What is density estimation?
The probability density function is a fundamental concept in statistics. Consider any random quantity X that has probability density function f. Specifying the function f gives a natural description of the distribution of X, and allows probabilities associated with X to be found from the relation
|
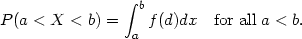
Suppose, now, that we have a set of observed data points assumed to be a sample from an unknown probability density function. Density estimation, as discussed in this book, is the construction of an estimate of the density function from the observed data. The two main aims of the book are to explain how to estimate a density from a given data set and to explore how density estimates can be used, both in their own right and as an ingredient of other statistical procedures.
One approach to density estimation is parametric. Assume that the
data are drawn from one of a known parametric family of distributions,
for example the normal distribution with mean µ and variance
2. The
density f underlying the data could then be estimated by finding
estimates of µ and
2 from the
data and substituting these estimates
into the formula for the normal density. In this book we shall not be
considering parametric estimates of this kind; the approach will be
more non parametric in that less rigid assumptions will be made about
the distribution of the observed data. Although it will be assumed
that the distribution has a probability density f, the data will be
allowed to speak for themselves in determining the estimate of f more
than would be the case if f were constrained to fall in a given
parametric family.
Density estimates of the kind discussed in this book were first proposed by Fix and Hodges (1951) as a way of freeing discriminant analysis from rigid distributional assumptions. Since then, density estimation and related ideas have been used in a variety of contexts, some of which, including discriminant analysis, will be discussed in the final chapter of this book. The earlier chapters are mostly concerned with the question of how density estimates are constructed. In order to give a rapid feel for the idea and scope of density estimation, one of the most important applications, to the exploration and presentation of data, will be introduced in the next section and elaborated further by additional examples throughout the book. It must be stressed, however, that these valuable exploratory purposes are by no means the only setting in which density estimates can be used.