2.8. Maximum penalized likelihood estimators

The methods discussed so far are all derived in an ad hoc way from the definition of a density. It is interesting to ask whether it is possible to apply standard statistical techniques, like maximum likelihood, to density estimation. The likelihood of a curve g as density underlying a set of independent identically distributed observations is given by

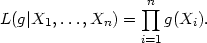
This likelihood has no finite maximum over the class of all densities. To see this, let _h be the naive density estimate with window width 1/2 h; then, for each i,

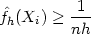
and so

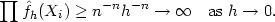
Thus the likelihood can be made arbitrarily large by taking densities approaching the sum of delta functions as defined in (2.7) above, and it is not possible to use maximum likelihood directly for density estimation without placing restrictions on the class of densities over which the likelihood is to be maximized.

There are, nevertheless, possible approaches related to maximum likelihood. One method is to incorporate into the likelihood a term which describes the roughness - in some sense - of the curve under consideration. Suppose R(g) is a functional which quantifies the roughness of g. One possible choice of such a functional is

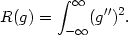
(2.11)

Define the penalized log likelihood by

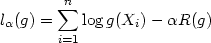
(2.12)

where is a positive smoothing parameter.

The penalized log likelihood can be seen as a way of quantifying the conflict between smoothness and goodness-of-fit to the data, since the log likelihood term log g(X_i) measures how well g fits the data. The probability density function is said to be a maximum penalized likelihood density estimate if it maximizes l(g) over the class of all curves g which satisfy _- g = 1, g(x) 0 for all x, and R(g) < . The parameter controls the amount of smoothing since it determines the `rate of exchange' between smoothness and goodness-of-fit; the smaller the value of , the rougher - in terms of R() - will be the corresponding maximum penalized likelihood estimator. Estimates obtained by the maximum penalized likelihood method will, by definition, be probability densities. Further details of these estimates will be given in Section 5.4.