


Excellent introductions are provided in textbooks such as those of Spitzer (1978), Aller (1984) or Osterbrock (1989). Here, we simply emphasize the properties to bear in mind when dealing with abundance determinations.
1.1. Ionization and recombination
1.1.1. Global ionization budget
Consider a source of photons surrounded by a cloud of nebular gas. The gas particles are ionized by those photons with energies above the ionization threshold. Once ionized, the particles tend to recombine with the free electrons, and an equilibrium stage is eventually established in which the rate of ionization equals the rate of recombination for each species.
Closer to the source, the density of ionizing photons is larger, therefore the resulting ionization state of the gas is higher. If there is enough nebular matter, all the ionizing photons can be absorbed, producing an ionization bounded nebula. If not, the nebula is called density bounded.
It is the most abundant species, (H and He in general, but this could be C, N, O in hydrogen-poor material) which absorb most of the Lyman continuum photons from the ionizing source, and thus define the size of the ionized region in the ionization bounded case.
In an ionization bounded nebula purely composed of hydrogen, the total number of recombinations per unit time balances the total number of photons with energies above 13.6 eV emitted per unit time either by the star, or during recombination to the ground level. One has:
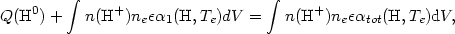 |
(1.1) |
where
Q(H0) is the total number of photons with
energies above 13.6 eV emitted by the star per second;
n(H+) is the number
density of H ions, ne is the electron density,
 is the
volume filling factor of the nebular gas;
is the
volume filling factor of the nebular gas;
 1(H,
Te) is
the H recombination coefficient to the ground level while
1(H,
Te) is
the H recombination coefficient to the ground level while
 tot(H,
Te) is the total H recombination
coefficient, which are both roughly inversely proportional to the electron
temperature Te. The integrations are
performed over the nebular volume.
tot(H,
Te) is the total H recombination
coefficient, which are both roughly inversely proportional to the electron
temperature Te. The integrations are
performed over the nebular volume.
In the case of a constant density nebula with constant filling factor, the radius of the ionized region, or Strömgren radius is then:
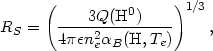 |
(1.2) |
where  B(H,
Te) is the H recombination coefficient to the excited
states (in this equation, Te represents an average
electron temperature of the nebula).
The thickness of the transition region between the fully ionized zone
and the neutral zone is approximately one mean free path of an
ionizing photon d = 1/n(H0)
B(H,
Te) is the H recombination coefficient to the excited
states (in this equation, Te represents an average
electron temperature of the nebula).
The thickness of the transition region between the fully ionized zone
and the neutral zone is approximately one mean free path of an
ionizing photon d = 1/n(H0)

 , where
, where

 is the hydrogen
photoionization cross section at the
typical frequency of the photons reaching the ionization front. This
thickness is generally much smaller than the size of the nebula and
justifies the concept of a Strömgren sphere. There are however
cases when the transition region might be extended, such as in
diffuse media or when the ionizing radiation field contains a large
amount of X-ray photons (which are less efficiently absorbed by hydrogen).
is the hydrogen
photoionization cross section at the
typical frequency of the photons reaching the ionization front. This
thickness is generally much smaller than the size of the nebula and
justifies the concept of a Strömgren sphere. There are however
cases when the transition region might be extended, such as in
diffuse media or when the ionizing radiation field contains a large
amount of X-ray photons (which are less efficiently absorbed by hydrogen).
During the recombination process captures to the excited levels
decay to lower levels by radiative transitions. The total luminosity of
the H line is
thus
line is
thus
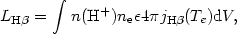 |
(1.3) |
where jH (Te) is the emission coefficient of
H
(Te) is the emission coefficient of
H and is
roughly proportional to
and is
roughly proportional to
 B(H).
Therefore the total luminosity in
H
B(H).
Therefore the total luminosity in
H in an
ionization bounded nebula is a direct measure of
Q(H0). At Te = 104
K, it is given by:
in an
ionization bounded nebula is a direct measure of
Q(H0). At Te = 104
K, it is given by:
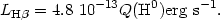 |
(1.4) |
In the case of a density bounded nebula, though, some ionizing photons
escape and L(H ) is then given by:
) is then given by:
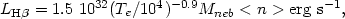 |
(1.5) |
where Mneb is the nebular mass in solar units and < n > is defined as:
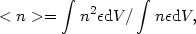 |
(1.6) |
assuming that in the nebula n(H+) =
ne = n(H)
 n.
n.
Thus, in the density bounded case, the total
H luminosity
does not say anything about
Q(H0), except that
Q(H0) has to be larger than the value
required to obtain the observed luminosity in
H
luminosity
does not say anything about
Q(H0), except that
Q(H0) has to be larger than the value
required to obtain the observed luminosity in
H . For a
given total nebular mass,
LH
. For a
given total nebular mass,
LH is larger for denser nebulae, since recombinations
are then more frequent.
is larger for denser nebulae, since recombinations
are then more frequent.
For nebulae composed of pure hydrogen, the maximum ionizable mass of gas for a given value of Q(H0) is, at Te = 104 K:
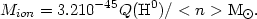 |
(1.7) |
The following table gives the values of Mion for a
typical PN, an H II region ionized by an O7 star, and a
giant H II
region ionized by a cluster of stars representing a total mass of
104
M (a Salpeter
mass function
is assumed and the star masses range between 1 and 100
M
(a Salpeter
mass function
is assumed and the star masses range between 1 and 100
M ).
).
| Q(H0) | M |
Mion | Mion | |
| n = 102 cm-3 | n = 104 cm-3 | |||
| planetary nebula | 31047 ph s-1 | 0.6
M |
10
M |
10-1
M |
| single star H II region | 31048 ph s-1 | 30
M |
102
M |
1
M |
| giant H II region | 31050 ph s-1 | 104
M |
104
M |
102
M |
The surface brightness of an object is an important parameter from the observational point of view. Indeed, for extended objects, it determines the detectability or the quality of the spectra. For illustrative purposes, let us consider here the simple case of an homogeneous sphere and define:
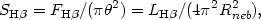 |
(1.8) |
where FH is the observed
H
is the observed
H flux,
flux,
 is the angular
radius of the nebula and Rneb its physical radius.
With the help of the previous equations one obtains for the ionization
bounded case:
is the angular
radius of the nebula and Rneb its physical radius.
With the help of the previous equations one obtains for the ionization
bounded case:
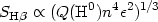 |
(1.9) |
and for the density bounded case:
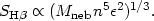 |
(1.10) |
Thus better data will be obtainable for objects of higher densities, and objects with higher Mneb or Q(H0).
The number fractions of He and heavy elements (C, N, O...) (1) in real nebulae are about 10% and 0.1% respectively. Helium, although ten times less abundant than hydrogen, is the dominant source of absorption of photons at energies above 24.4 eV. For order of magnitudes estimates, however, the formulae given above can still be used, since each recombination of He roughly produces one photon that can subsequently be absorbed only by hydrogen. The same remark generally holds for photons above 54.4 eV in the spectra of PNe with hot nuclei (see however Stasinska & Tylenda 1986). Naturally, for detailed studies, a photoionization modelling is necessary that takes into account properly the transfer of the photons arising from the recombination to He0 and He+.
1 It is a tradition in nebular studies, to refer to elements other than H and He as "heavy elements" or "metals". Back.