1.1.2. The ionization structure

At a distance r from the ionizing source, the number densities n(X_i^j) and n(X_i^{j + 1}) of the ions X_i^j and X_i^{j + 1} are schematically related by the following expression:

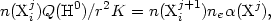(1.11)

where K is a factor taking into account the frequency distribution of the ionizing radiation field and the absorption cross section (note that, for simplicity, the charge exchange process is not included in this equation). Of course, ions X_i^{j + 1} can exist only if the radiation field contains photons able to produce these ions, and the ratio n(X_i^{j + 1})/n(X_i^j) will be higher for higher effective temperatures of the ionizing source.

Integrating Eq. (1.11) over the nebular volume and using Eq. (1.2), it can be shown that, for a spherical nebula of constant density and filling factor and with an ionizing radiation of given effective temperature, the average ionic ratios are proportional to (Q(H⁰)n²)^1/3. In other words, a nebula of density n = 10⁴ cm^-3 ionized by one star with T = 50000 K will have the same ionization structure as a nebula of density n = 10² cm^-3 ionized by one hundred such stars.

The ionization parameter is usually defined by

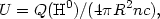(1.12)

where R is either the Strömgren radius, or a typical distance from the gas cloud to the ionizing star, and c is the speed of light. U is thus directly proportional to (Q(H⁰)n^21/3 in the case of a constant density sphere and this parameter describes the ionization structure.

It is important to be aware that equation (1.12) shows that at a given distance from the source, ionization drops when the density is increased locally (like in the case of a density clump). On the other hand, of two nebulae with uniform density and ionized by the same star, the highest average ionization will occur for the densest one.

The presence of intense lines of low ionized species such as [N II] 6584, [S ii] 6716, 6731, [O i] 6300, is often considered in the literature as a signature of the presence of shocks. Shock models indeed predict that these lines are strong, but it must be kept in mind that pure photoionization models can also produce strong low ionization lines. This is for example the case for nebulae containing regions of low ionization due to gas compression (e.g. Dopita 1997 Stasinska & Schaerer 1999). Another example is that of ebulae excited by very high energy photons, for which the absorption cross-section is small and which induce a warm, only partially ionized zone.