1.2. Heating and cooling

During the photoionization process, the absorption of a photon creates a free electron which rapidly shares its energy with the other electrons present in the gas by elastic collisions, and thus heats the gas. The energy gains are usually dominated by photoionization of hydrogen atoms, although photoionization of helium contributes significantly. Intuition might suggest that T_e will decrease away from the ionizing source, since the ionizing radiation field decreases because of geometrical dilution and absorption in the intervening layers. This is actually not the case. The total energy gains per unit volume and unit time at a distance r from the ionizing source are schematically given by:

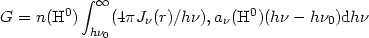(1.13)

where

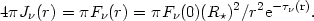(1.14)

If ionization equilibrium is achieved in each point of the nebula, one has (in the "on-the-spot case")

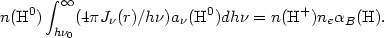(1.15)

Therefore, G can be written

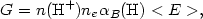(1.16)

where

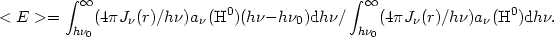(1.17)

Thus < E > can be seen as the average energy gained per photoionization, and is roughly independent of r. It can be shown (see e.g. Osterbrock 1989), that when the ionization source is a blackbody of temperature T, one has < E > (3/2)kT. Therefore:

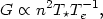(1.18)

meaning that the energy gains are roughly proportional to the temperature of the ionizing stars.

Thermal losses in nebulae occur through recombination, free-free radiation and emission of collisionally excited lines. The dominant process is usually due to collisional excitation of ions from heavy elements (with O giving the largest contribution, followed by C, N, Ne and S). Indeed, these ions have low-lying energy levels which can easily be reached at nebular temperatures. The excitation potentials of hydrogen lines are much higher, so that collisional excitation of H⁰ can become important only at high electron temperatures.

For the transition l of ion j of an element Xⁱ, in a simple two-level approach and when each excitation is followed by a radiative deexcitation, the cooling rate can be schematically written as

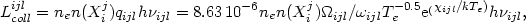(1.19)

where _ijl is the collision strength, _ijl is the statistical weight of the upper level, and _ijl is the excitation energy.

If the density is sufficiently high, some collisional deexcitation may occur and cooling is reduced. In the two-level approach one has:

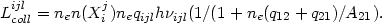(1.20)

So, in a first approximation, one can write that the electron temperature is determined by

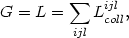(1.21)

where G is given by Eq. (1.18) and L_coll^ijl by Eq. (1.20).

The following properties of the electron temperature are a consequence of the above equations:

- T_e is expected to be usually rather uniform in nebulae, its variations are mostly determined by the mean energy of the absorbed stellar photons, and by the populations of the main cooling ions. It is only at high metallicities (over solar) that large T_e gradients are expected: then cooling in the O⁺⁺ zone is dominated by collisional excitation of fine structure lines in the ground level of O⁺⁺, while the absence of fine structure lines in the ground level of O⁺ forces the temperature to rise in the outer zones (Stasinska 1980a, Garnett 1992).

- For a given T , T_e is generally lower at higher metallicity.

- For a given metallicity, T_e is generally lower for lower T .

- For a given T and given metallicity, T_e increases with density in regions where n is larger than a critical density for collisional deexcitation of the most important cooling lines (around 5 × 10² - 10³ cm^-3).