2. BIG BANG NUCLEOSYNTHESIS AND THE PRIMORDIAL ABUNDANCES

Since the early universe is hot and dense, interactions among the various particles present are rapid and equilibrium among them is established quickly. But, as the universe expands and cools, there are departures from equilibrium; these are at the core of the most interesting themes of our story.

2.1. An Early Universe Chronology

At temperatures above a few MeV, when the universe is tens of milliseconds old, interactions among photons, neutrinos, electrons, and positrons establish and maintain equilibrium (T = T = T_e). When the temperature drops below a few MeV the weakly interacting neutrinos decouple, continuing to cool and dilute along with the expansion of the universe (T a^-1, n T³, and T⁴).

2.1.1. Neutron - Proton Interconversion

Up to now we haven't considered the baryon (nucleon) content of the universe. At these early times there are neutrons and protons present whose relative abundance is determined by the usual weak interactions

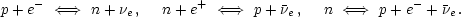(1.24)

As time goes by and the universe cools, the lighter protons are favored over the heavier neutrons and the neutron-to-proton ratio decreases, initially as n / p exp(- m / T), where m = 1.29 MeV is the neutron-proton mass difference. As the temperature drops below roughly 0.8 MeV, when the universe is roughly one second old, the rate of the two-body collisions in eq. 24 becomes slow compared to the universal expansion rate and deviations from equilibrium occur. This is often referred to as "freeze-out", but it should be noted that the n / p ratio continues to decrease as the universe expands, albeit at a slower rate than if the ratio tracked the exponential. Later, when the universe is several hundred seconds old, a time comparable to the neutron lifetime (_n = 885.7 ± 0.8 sec.), the n/p ratio resumes falling exponentially: n / p exp(-t / _n). Notice that the n/p ratio at BBN depends on the competition between the weak interaction rates and the early universe expansion rate so that any deviations from the standard model (e.g. + _X) will change the relative numbers of neutrons and protons available for building more complex nuclides.