Copyright © 1996 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1996. 34:
155-206 Copyright © 1996 by Annual Reviews. All rights reserved |
2.2. Large-Scale Field Patterns
The plane of polarization of a linearly polarized radio wave
rotates when the wave passes through a plasma with a regular magnetic
field. The rotation angle

 increases with the integral of
ne B||
along the line of sight (where ne is the
thermal electron density and B|| is the
component of the total magnetic field along the line of sight) and with
increases with the integral of
ne B||
along the line of sight (where ne is the
thermal electron density and B|| is the
component of the total magnetic field along the line of sight) and with
 2 (where
2 (where
 is the wavelength of
observation). The quantity
is the wavelength of
observation). The quantity

 /
/

 2 is called
the rotation measure, RM. The observed RM is sensitive to the regular
magnetic field
2 is called
the rotation measure, RM. The observed RM is sensitive to the regular
magnetic field
 || because
the random fields B|| mostly cancel.
The sign of RM allows the two opposite directions of
|| because
the random fields B|| mostly cancel.
The sign of RM allows the two opposite directions of
 || to be
distinguished.
An accurate determination of RM requires observations at (at least)
three wavelengths because the observed orientation of the
polarization plane is ambiguous by a multiple of
± 180° (see
Ruzmaikin & Sokoloff
1979).
Unlike equipartition estimates, which are insensitive to the presence
of field reversals within the volume observed by the telescope beam,
the observed value of Faraday rotation
will decrease with increasing number of reversals.
|| to be
distinguished.
An accurate determination of RM requires observations at (at least)
three wavelengths because the observed orientation of the
polarization plane is ambiguous by a multiple of
± 180° (see
Ruzmaikin & Sokoloff
1979).
Unlike equipartition estimates, which are insensitive to the presence
of field reversals within the volume observed by the telescope beam,
the observed value of Faraday rotation
will decrease with increasing number of reversals.
Although the filled apertures of single-dish telescopes are sensitive to all spatial structures above the resolution limit, synthesis instruments such as the VLA cannot provide interferometric data at short spacings. This shortcoming results in some blindness to extended emission. Missing large-scale structures in maps of Stokes parameters Q and U can systematically distort the polarization angles and hence the RM distribution, so that the inclusion of additional data from single-dish telescopes in all Stokes parameters is required. In Section 3.4 (Figure 3) we show the result of such a successful combination by using a maximum-entropy method.
A convenient general way to parameterize the global magnetic field
(irrespective of its origin) is by Fourier decomposition in terms
of the azimuthal angle
 measured in
the plane of the galaxy,
measured in
the plane of the galaxy,
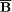 =
=
 m
m
 m
exp(i m
m
exp(i m  ).
In practice, observations are analyzed within rings (centered at the
galaxy's center) whose width is chosen to be consistent with the
resolution of the observations. The result is a set of Fourier
coefficients of the large-scale magnetic field for each ring.
Usually, a combination of m = 0 and m = 1
modes is enough to provide a statistically satisfactory fit to the
data. This is a remarkable indication of the presence of genuine
global magnetic structures in spiral galaxies.
).
In practice, observations are analyzed within rings (centered at the
galaxy's center) whose width is chosen to be consistent with the
resolution of the observations. The result is a set of Fourier
coefficients of the large-scale magnetic field for each ring.
Usually, a combination of m = 0 and m = 1
modes is enough to provide a statistically satisfactory fit to the
data. This is a remarkable indication of the presence of genuine
global magnetic structures in spiral galaxies.
All observed magnetic fields have significant radial and azimuthal components: The magnetic lines of the regular field are spirals (Section 8.3). We distinguish between spiral structures that can be considered as basically axisymmetric (ASS), and basically antisymmetric or bisymmetric (BSS), with respect to rotation by 180°. Note that higher azimuthal Fourier modes are expected to be superimposed on these dominant ones, but these should have relatively small amplitudes. Fields containing several Fourier components of significant amplitude have mixed spiral structure (MSS); this might be considered to be a combination of ASS and BSS.
A further classification of magnetic structures according to their symmetry with respect to the galaxy's midplane distinguishes symmetric S (i.e. even parity or quadrupole) from antisymmetric (odd parity or dipole) modes A.
Mixed-parity distributions (M), in which the magnetic fields are neither even nor odd but are superpositions, are also possible. This notation is supplemented with a value of the azimuthal wave number m, e.g. S0 means a quadrupole axisymmetric field. The notation used in discussions of global magnetic structures in spiral galaxies in presented in Table 1.
| Vertical | Azimuthal structure | ||
|---|---|---|---|
| structure | ASS | BSS | MSS |
|
| |||
| Even | S0 | S1 | S0 + S1 |
| Odd | A0 | A1 | A0 + A1 |
| Mixed | M0 | M1 | M0 + M1 |
|
| |||
An ASS (BSS) field produces a
2 -periodic
(
-periodic
( -periodic) distribution of RM
along
-periodic) distribution of RM
along
 (Sofue et al 1986,
Krause 1990,
Wielebinski & Krause
1993).
For the m = 0 mode, the phase of the variation of RM
with
(Sofue et al 1986,
Krause 1990,
Wielebinski & Krause
1993).
For the m = 0 mode, the phase of the variation of RM
with  is equal
to the magnetic pitch angle,
p = arctan(
is equal
to the magnetic pitch angle,
p = arctan( r /
r / 
 ).
Using the observed azimuthal distribution of RM in a galaxy,
the structure of the line-of-sight component of a large-scale
magnetic field can be studied. This method is difficult to apply if
the data suffer from Faraday depolarization, if
the regular field is not parallel to the plane of the galaxy,
if its pitch angle in the disk is not constant,
or if the disk is surrounded by a halo with magnetic fields of
comparable strengths.
).
Using the observed azimuthal distribution of RM in a galaxy,
the structure of the line-of-sight component of a large-scale
magnetic field can be studied. This method is difficult to apply if
the data suffer from Faraday depolarization, if
the regular field is not parallel to the plane of the galaxy,
if its pitch angle in the disk is not constant,
or if the disk is surrounded by a halo with magnetic fields of
comparable strengths.
A more direct method of analysis considers polarization
angles  without converting
them into Faraday rotation measures
(Ruzmaikin et al 1990;,
Sokoloff et al 1992;
EM Berkhuijsen et al, in preparation)
There are three main contributions to the observed polarization angle:
without converting
them into Faraday rotation measures
(Ruzmaikin et al 1990;,
Sokoloff et al 1992;
EM Berkhuijsen et al, in preparation)
There are three main contributions to the observed polarization angle:
 =
=
 0 + RM
0 + RM
 2 +
RMfg
2 +
RMfg
 2,
where
2,
where  0 is determined
by the transverse magnetic field in the galaxy, RM is
associated with Faraday rotation by the line-of-sight
magnetic field in the galaxy, and RMfg is the foreground
rotation measure. Thus, a direct
analysis of
0 is determined
by the transverse magnetic field in the galaxy, RM is
associated with Faraday rotation by the line-of-sight
magnetic field in the galaxy, and RMfg is the foreground
rotation measure. Thus, a direct
analysis of  patterns
at several wavelengths allows a self-consistent study of
all three components of the regular magnetic field. Another
advantage of this method is that complicated magnetic structures
along the line of sight can be studied. Implementations of this
method employ consistent statistical tests such as the
patterns
at several wavelengths allows a self-consistent study of
all three components of the regular magnetic field. Another
advantage of this method is that complicated magnetic structures
along the line of sight can be studied. Implementations of this
method employ consistent statistical tests such as the
 2 and
Fisher criteria, thereby allowing the reliability of the results to
be assessed.
2 and
Fisher criteria, thereby allowing the reliability of the results to
be assessed.
Note that Faraday rotation analysis yields an average value,
<neB||>. Information on
 || can be
extracted
only if a reliable model for the distribution of ne is
available, which is often not the case. If, for example, the thermal gas
has a low filling factor, any result concerning
|| can be
extracted
only if a reliable model for the distribution of ne is
available, which is often not the case. If, for example, the thermal gas
has a low filling factor, any result concerning
 ||
may not be representative.
||
may not be representative.