Copyright © 1996 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1996. 34:
155-206 Copyright © 1996 by Annual Reviews. All rights reserved |
4.3. Treatment of Galactic Turbulence
Several basic gas components are involved in galactic turbulence.
The disk consists of warm gas, interspersed by cold clouds and hot bubbles.
Hot bubbles result from local heating (e.g. OB associations and
supernova and superbubble explosions) and eject hot gas into the halo
(galactic fountains). These violent motions, in addition to stellar winds,
help to drive the turbulence.
Furthermore, random motions of molecular clouds may stir up the warm gas,
because they are dynamically coupled by magnetic field lines.
The Parker instability may also be a source of turbulence, or it may at
least act as an agent causing the movement of flux tubes and thereby
generate an  -effect
(Parker 1992,
Hanasz & Lesch
1993).
In the model of
Vázquez-Semadeni et al
(1995),
the turbulence is driven
by gravity and density gradients that result from interstellar cooling
and heating processes.
-effect
(Parker 1992,
Hanasz & Lesch
1993).
In the model of
Vázquez-Semadeni et al
(1995),
the turbulence is driven
by gravity and density gradients that result from interstellar cooling
and heating processes.
To understand the effect of these different gas components on the magnetic field we need to discuss the coupling of the magnetic field to those components. The magnetic fields in the hot component are rapidly ejected into the halo. They are then no longer directly important for magnetic processes in the disk, but are essential in the galactic halo. Clouds could be more important, because a large-scale field would be dragged with the gas into these clouds as they form, and the cloud motions would entangle the magnetic field lines (Beck 1991). This process is of only limited duration, because ambipolar diffusion (Mestel 1966) would decouple the clouds from the field on a timescale of 107 yr.
The outcome is that for most of the time the magnetic field remains attached to the diffuse ionized gas, and, to the extent that the field is associated with clouds, the effect of the clouds is to contribute to the turbulent dynamics of the magnetic field lines. Even if this is an important contributor to the chaotic driving of field lines (in addition to the turbulence mentioned above), it is reasonable to assume that the magnetic field in a galactic disk is on average linked to the warm, ionized medium and perhaps also to the warm neutral medium, both of which are in a turbulent state.
Dynamo action is well established from numerical turbulence simulations.
In the absence of (rotational) velocity shear, the magnetic field is
very intermittent
(Meneguzzi et al 1981).
In the presence of rotational shear, the resulting magnetic shear
instability (e.g.
Balbus & Hawley 1992
can lead to strong large-scale fields
(Brandenburg et al
1995a).
This mechanism yields coherent fields similar to those in ordinary

 -dynamos.
-dynamos.
The classical  -effect
quantifies the field-aligned electromotive force
resulting from magnetic field lines twisted by the turbulence (cf
simulations
by Otmianowska-Mazur &
Urbanik 1994).
In the original picture the dynamics of these field lines is governed
by external turbulent motions.
Parker (1992)
discussed a new, perhaps more appropriate, concept in which the
motions result mostly from the dynamics of magnetic field lines themselves.
The concept of an
-effect
quantifies the field-aligned electromotive force
resulting from magnetic field lines twisted by the turbulence (cf
simulations
by Otmianowska-Mazur &
Urbanik 1994).
In the original picture the dynamics of these field lines is governed
by external turbulent motions.
Parker (1992)
discussed a new, perhaps more appropriate, concept in which the
motions result mostly from the dynamics of magnetic field lines themselves.
The concept of an
 -effect seems, however,
sufficiently
robust so that the form of the basic equations is always the same. In
fact, the
-effect seems, however,
sufficiently
robust so that the form of the basic equations is always the same. In
fact, the  -effect is
only one of many effects relating the mean
emf
-effect is
only one of many effects relating the mean
emf 

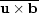 to the mean magnetic field and its derivatives.
If the mean field is not too intermittent, we can expand
to the mean magnetic field and its derivatives.
If the mean field is not too intermittent, we can expand
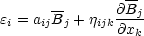 |
(1) |
(Krause & Rädler
1980),
neglecting higher derivatives of
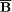 . This relation is
used when solving the induction equation for the mean magnetic field,
. This relation is
used when solving the induction equation for the mean magnetic field,
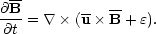 |
(2) |
The mean velocity 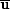 comprises both the rotational
velocity, as well as galactic winds and any other large-scale flows.
This is where the observed rotation curves and other large-scale flow
components of individual galaxies enter into the theory and models.
comprises both the rotational
velocity, as well as galactic winds and any other large-scale flows.
This is where the observed rotation curves and other large-scale flow
components of individual galaxies enter into the theory and models.
The  ij
and
ij
and
 ijk tensors in (1) are anisotropic
(Ferriére 1993,
Kitchatinov et al 1994).
Anisotropies can arise from stratification, rotation, shear, and
magnetic fields. Stratification and rotation are most important, because
without them there would be no
ijk tensors in (1) are anisotropic
(Ferriére 1993,
Kitchatinov et al 1994).
Anisotropies can arise from stratification, rotation, shear, and
magnetic fields. Stratification and rotation are most important, because
without them there would be no


 component,
which is
needed to regenerate poloidal magnetic fields from
component,
which is
needed to regenerate poloidal magnetic fields from

 .
An important contribution to
.
An important contribution to
 ijk comes from isotropic
turbulent magnetic diffusion,
ijk comes from isotropic
turbulent magnetic diffusion,
 ijk
ijk
 t,
where
t,
where
 t is
the turbulent magnetic diffusivity.
Explicit expressions in the framework of the first-order smoothing
approximation (FOSA) were first derived by
Steenbeck et al (1966),
Krause (1967),
and more recently by
Rüdiger &
Kitchatinov (1993). They find expressions of the form
t is
the turbulent magnetic diffusivity.
Explicit expressions in the framework of the first-order smoothing
approximation (FOSA) were first derived by
Steenbeck et al (1966),
Krause (1967),
and more recently by
Rüdiger &
Kitchatinov (1993). They find expressions of the form
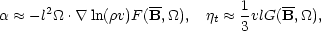 |
(3) |
where l is the correlation length of the turbulence
 stands for
stands for


 ,
and F
and G are certain ("quenching") functions. The stratification of
,
and F
and G are certain ("quenching") functions. The stratification of
 v is
important, because it breaks the symmetry between upward and downward
motions. If h is the scale height, a rough estimate gives
v is
important, because it breaks the symmetry between upward and downward
motions. If h is the scale height, a rough estimate gives
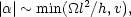 |
(4) |
which ensures that
 does not exceed
v (e.g.
Zeldovich et al 1983).
does not exceed
v (e.g.
Zeldovich et al 1983).
The FOSA is valid either for small magnetic Reynolds numbers (which is
irrelevant here) or in the limit of short correlation times (which is also
not well satisfied in the ISM). However, although higher order terms may
become important, they affect the results only quantitatively
(Zeldovich et al 1988,
Carvalho 1992).
There are independent attempts to compute the transport coefficients
resulting from evolving flux tubes
(Hanasz & Lesch
1993)
and from expanding
supernovae and superbubbles rather than from turbulence
(Ferriére 1993,
Kaisig et al 1993).
The resulting values of  and
and
 t
are smaller than those expected from interstellar turbulence,
suggesting that explosions are of lesser importance.
t
are smaller than those expected from interstellar turbulence,
suggesting that explosions are of lesser importance.
Turbulent diamagnetism
(Zeldovich 1957)
can be represented as a macroscopic velocity,
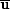 dia = -1/2
dia = -1/2

 t
(Roberts & Soward
1975,
Kitchatinov &
Rüdiger 1992).
It tends to expel magnetic fields from regions wher
t
(Roberts & Soward
1975,
Kitchatinov &
Rüdiger 1992).
It tends to expel magnetic fields from regions wher
 t
is large.
This term can be considered as a contribution to the antisymmetric part of
t
is large.
This term can be considered as a contribution to the antisymmetric part of
 ij
(Rädler 1969).
Additional effects of this kind are magnetic buoyancy
(Moss et al 1990)
and topological pumping (Section 7.2).
ij
(Rädler 1969).
Additional effects of this kind are magnetic buoyancy
(Moss et al 1990)
and topological pumping (Section 7.2).