Annu. Rev. Astron. Astrophys. 1996. 34: 155-206 Copyright © 1996 by Annual Reviews. All rights reserved

4.4. Basic Galactic Dynamo Models

The simplest form of the mean field (² ) dynamo equation (2) that retains the basic physics (e.g. Parker 1979, Roberts & Soward 1992) is, in dimensionless form,

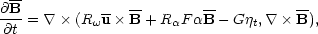(5)

where F(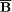, ) = (1 + 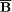² / B_eq²)^-1 is the simplest form of "-quenching" and G(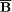, ) = 1. Distances and times are measured in units of h_* and h_*² / _t*, respectively, where 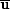= × r and and _t are normalized by appropriately chosen characteristic values denoted by asterisks. Dimensionless numbers

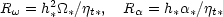(6)

characterize the amplification of magnetic field by shearing of the mean velocity field and the -effect, respectively. Using Equation (3), and _t can be expressed through observable parameters of the galaxies such as the rotation curve, rms velocity and scale, and the thickness of the ionized disk (a function of r). The quenching effects also require that the gas density is specified as a function of position. Equation (5) must be supplemented by boundary conditions. In models that treat the disk alone, these are usually vacuum boundary conditions in which one assumes that the turbulent magnetic diffusivity outside the disk is infinite. This proves to be a reasonable approximation to reality (Moss & Brandenburg 1992), as _t varies by perhaps a factor of about 50 between the disk and the halo (see Brandenburg et al 1993, Poezd et al 1993). However, more advanced treatments employ the embedded disk model (Stepinski & Levy 1988). This includes a spherical galactic halo and appropriate boundary conditions are imposed at the surface of the halo, whereas the disk is modeled by appropriate distributions of 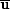, , and _t. This concept has proved sufficiently adaptable to accommodate developing requirements, such as the inclusion of a flared disk, an -effect extending into the halo (Section 7.1), and/or a galactic wind (Section 7.2).

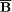
Initial conditions for (5) are often chosen to correspond to a weak seed field. Exponentially growing solutions then arise, exp( t), provided the dynamo number D = R R exceeds a certain value D_crit 10. Using Equation (3) one can show that D 9(h_{* *} / v)². For h_* 500 pc, _* 20 km s^-1 kpc^-1, and v 10 km s^-1 we obtain D 10, so that the dynamo is expected to operate under typical galactic conditions. For D >> D_crit, the growth rate is estimated as CD^1/2 _t / h_*² C(_{* *} h_*)^1/2, with C a quantity of order unity depending on the galaxy model. A typical model gives ^-1 5 × 10⁸ yr; this is a lower estimate for the dynamo timescale. [We note, however, that the timescale for the magnetic shear instability is the inverse Oort a-value (Balbus & Hawley 1992), which is somewhat shorter (10⁸ yr). This mechanism leads to dynamo action (Brandenburg et al 1995b) that would lower the effective value of ^-1.]

All classical dynamo models predict that the large-scale field in the outer parts of the disks in spiral galaxies has quadrupole (S0) symmetry, that is, both _r and are even in z, whereas _z is odd (Parker 1971, Vainshtein & Ruzmaikin 1971). This mode is dominant in a disk (but not in a sphere). A dipole (A0) mode, with both _r and odd in z and _z even, can be dominant near the axis of the disk. The large-scale field is amplified until becomes significantly quenched, which occurs when is of order B_eq, typically a few µG.

Field evolution is qualitatively different if the initial field is a random field with strength close to B_eq. There is then no kinematic stage, because -quenching is immediately important. The dynamo acts then to change the scale and spatial distribution of the field. An example of typical evolution of the magnetic field in a spiral galaxy as envisaged by the standard dynamo model is illustrated in Figure 7.

Figure 7. Face-on views showing the evolution of the magnetic field in a model of M83 (from KJ Donner & A Brandenburg, in preparation). The lower panel gives an edge-on view for t = 8.1 Gyr.

Over the past 5 to 10 years a large number of galactic dynamo models have been developed. The minimum ingredient of such models is a flat geometry. Such models were first computed in the 1970s, but computers can only now reach the regime applicable to the theory of asymptotically thin disks (Walker & Barenghi 1994 and references therein). Galactic models share the somewhat frustrating property that nonaxisymmetric solutions are always harder to excite than axisymmetric ones (Ruzmaikin et al 1988a, Brandenburg et al 1990, Moss & Brandenburg 1992). Not even the inclusion of anisotropies seems to change this conclusion (Meinel et al 1990). Stable nonaxisymmetric solutions have only been found if and _t vary azimuthally (Moss et al 1991, 1993a;, Panesar & Nelson 1992). The inclusion of nonlinear effects demonstrated that mixed parity states can persist over rather long times, even comparable with galactic lifetimes (Moss & Tuominen 1990, Moss et al 1993a). When -quenching is included (G 1), linear calculations show that A0 and S1 modes may be more readily excited (Elstner et al 1996).

In most of these models _ij and _ijk were adopted using qualitative forms of (3) and (4), calibrated by observations. Significant conceptual progress has been made recently by deriving all these functions consistently from the same turbulence model, which includes stratification of density and turbulent velocity, derived from a condition of hydrostatic equilibrium (Schultz et al 1994, Elstner et al 1996). One should not forget, however, that such models still rely on important approximations and simplifications (e.g. FOSA and the lack of a reliable turbulence model).