Annu. Rev. Astron. Astrophys. 1996. 34: 155-206 Copyright © 1996 by Annual Reviews. All rights reserved

5. ORIGIN OF GALACTIC MAGNETIC FIELDS

5.1. Cosmological Magnetic Fields

Zeldovich (1965) noted that a Friedmannian cosmology admits a weak uniform magnetic field given as an initial condition at the Big Bang (see also Zeldovich & Novikov 1982, LeBlanc et al 1995). A hypothetical homogeneous magnetic field in the Universe has been never detected and only its upper limits are available. A uniform magnetic field 10^-7 G at the present day would lead to anisotropy in the expansion of the Universe, thereby affecting nucleosynthesis (e.g. Cheng et al 1994, Grasso & Rubinstein 1995). Analysis of Faraday rotation measures of extragalactic sources gives a stronger upper limit of 10^-9-10^-10 G (Ruzmaikin & Sokoloff 1977). A magnetic field leads to transitions between left- and right-handed neutrinos (spin-flip) in the early Universe. Nucleosynthesis gives an upper limit to the abundance of right-handed neutrinos and thus yields the constraint

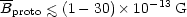(7)

for the present-day uniform cosmological field (Sciama 1994).

Taking a cosmological magnetic field as a given initial condition at the Big Bang is rather unsatisfactory. Furthermore, it is not clear whether a homogeneous magnetic field can be incorporated into modern quantum cosmology, where it cannot be prescribed as an initial condition.

Several mechanisms of small-scale magnetic field generation by quantum effects in the early Universe have been proposed (Turner & Widrow 1988, Quashnock et al 1989, Vachaspati 1991, Ratra 1992). The resulting spatial scales of cosmological magnetic fields are very small and, even after cosmological expansion, they are negligible in comparison with protogalactic scales.

The strength and scale of the relic magnetic field can be estimated as follows. As magnetic diffusion smoothes the field, its scale at time t will be about ( t)^1/2, where is the magnetic diffusivity, as the initial scale is much smaller. At the epoch of nucleosynthesis, the resulting scale is 10⁴ cm, corresponding to a scale l 10^-6 pc today. The same arguments as for Equation (7) give an upper limit on the magnetic field at nucleosynthesis of 10¹¹ G. With allowance for a change in the equation of state at t = t_* 10⁴ yr, the frozen-in magnetic field at time t is diluted by cosmological expansion to b(t_* / t)^4/3(1 min / t_*)^1/3. Since the protogalaxy includes (L / l)³ correlation cells, the average field strength is smaller by a factor (L / l)^-3/2. This yields the following upper limit on the average magnetic field at the scale of the protogalaxy at the present time,

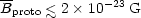(8)

(see Enqvist et al 1993, 1995). Thus either the cosmological magnetic field is exactly homogeneous, and then the restriction (7) applies, or the field was produced in the early Universe, and then it must satisfy (8). We should note that the above estimates neglect ohmic losses. These constraints do not apply to magnetic fields generated at later stages of cosmological evolution. Battery mechanisms can contribute at more recent epochs, giving (Mishustin & Ruzmaikin 1971, see also Harrison 1970, Baierlein 1978),

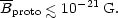(9)