Annu. Rev. Astron. Astrophys. 1996. 34: 155-206 Copyright © 1996 by Annual Reviews. All rights reserved

4.5. The Quenching Problem

In recent years the feedback of the magnetic field on the turbulent diffusion and the -effect has become a topic of major concern. Piddington (1970) was the first to suggest that for large magnetic Reynolds numbers the magnetic fluctuations would be strong enough to suppress turbulent diffusion. This idea was rejected by Parker (1973), who argued that the development of strong small-scale fields is limited by reconnection, so that they do not hinder turbulent mixing of field and fluid. In fact, without turbulent diffusion the galactic differential rotation would wind up the field so tightly that it would not resemble the magnetic field structure of any observed galaxy (Section 8.3).

The results of the two-dimensional numerical MHD experiment of Cattaneo & Vainshtein (1991) stimulated new interest in the problem of turbulent diffusion. They found that _t is suppressed according to _t = v l / (1 + R_m 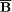² / B_eq²), where R_m = vL / is the magnetic Reynolds number based on the microscopic diffusivity. Evidently, _t would be significantly reduced when is comparable to R_m^-1/2 B_eq. In galaxies, R_m = (10¹⁷), so _t would essentially be zero. Even if we used a Reynolds number based on ambipolar diffusion, with R_m^AD O(10³), _t would still be too small. This type of quenching is much stronger than the "traditional" quenching (Moffatt 1972), so something seems to be wrong (e.g. Field 1996).

In three dimensions the turbulent motions would continue to entangle the magnetic field in the direction perpendicular to 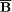(Krause & Rüdiger 1975, Parker 1992). This has now also been demonstrated numerically (Nordlund et al 1994) as well as analytically (Gruzinov & Diamond 1994). In other words, turbulent diffusion is really not significantly suppressed at field strengths somewhat below the equipartition value. The decay of sunspots is a good example of this (Krause & Rüdiger 1975).

Vainshtein & Cattaneo (1992), Tao et al (1993) suggested that the -effect might also be quenched dramatically, = _kin / (1 + R_m 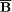² / B_eq²), where _kin is the kinematic value of Equation (3). The analysis of Gruzinov & Diamond (1994) seems to support this result. On the other hand, the simulations of Tao et al (1993), as well as unpublished simulations by A Brandenburg, are reminiscent of an earlier result by Moffatt (1979), that the -effect may fluctuate strongly and never converge to a finite value if R_m is large.

There is at present no conclusive resolution to this problem, but here are some possibilities: (a) The conventional -effect might still work in reality, but the method used to estimate from simulations is inappropriate (e.g. the boundary conditions preserve the magnetic flux, so the -effect is forced to have zero effect on the average field; or the computational domain might be too small compared to the eddy size). (b) The conventional -effect is really nonexistent, but instead some other mechanism (e.g. an inverse cascade mechanism, incoherent -effect, or cross-helicity effect) generates large-scale fields in conjunction with shear. (c) An important contribution to comes from the Parker instability: This mechanism would work especially for finite magnetic fields.

A somewhat different problem was raised by Kulsrud & Anderson (1992), who suggested that the growth of large-scale fields is suppressed by ambipolar diffusion at small scales. However, before we can draw any final conclusions, nonlinear effects need to be included. These can be important for two reasons: The inverse cascade process is inherently nonlinear, and nonlinear ambipolar diffusion can lead to sharp magnetic structures (Brandenburg & Zweibel 1995), which would facilitate fast reconnection and rapidly remove magnetic energy at small scales.

The problem raised by Vainshtein & Cattaneo (1992) is related to the assumption that most of the magnetic energy is at small scales, i.e. < B² >> > B². This, however, is only a result of linear theory and is not supported by observations (Section 3). A recent simulation by Brandenburg et al (1995a) is relevant in this context. Here a large-scale field is generated with <B²> / <B²> 0.5 >> R_m^-1/2 0.1. The dynamo works even in the presence of ambipolar diffusion, which Kulsrud & Anderson (1992) thought to be effective in destroying large-scale dynamo action. Here, the incoherent -effect is much larger than the coherent effect, but the estimated value of the dynamo number is nevertheless above the critical value, suggesting that conventional dynamo action might also be at work.