Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

2.4. Initial Conditions

Initial conditions for simulations of structure formation consist of specifying the background cosmological model and the perturbations imposed on this background. The background model is generally taken to be a spatially flat or open Robertson-Walker spacetime with specified composition of dark matter, baryons, a possible cosmological constant, etc. Specifying such a model requires more than just the two numbers H₀ and (or the deceleration parameter q₀); at the very least the amount and nature of dark matter must be given (Trimble 1987).

At very high redshift, e.g. at z 1100 when recombination has occurred and photons decouple from baryons, small-amplitude ("linear") density fluctuations were present in each component (baryons, photons, massless neutrinos, dark matter). The statistical nature of these fluctuations depends, of course, on how they were generated. Two classes of early universe models are widely considered to provide plausible mechanisms: inflation (Guth 1981) and topological defects (Vilenkin & Shellard 1994). Inflation predicts Gaussian fluctuations, while defect models are non-Gaussian.

Gaussian fluctuations are simple, as they are specified fully by one function, the power spectrum P(k). In Gaussian models, the fluctuations are set down ab initio (perhaps 10^-35 s after the Big Bang) and evolve straightforwardly thereafter. In real space, the joint probability distribution of density fluctuations at N points is a multidimensional Gaussian (i.e. multivariate normal distribution). Because the covariance matrix of this Gaussian becomes diagonal in Fourier space, it is very easy to sample a Gaussian random field by sampling its Fourier components on a Cartesian lattice (Peacock & Heavens 1985, Bardeen et al 1986). Salmon (1996) has implemented an alternative method based on convolving a white noise process, with the advantage that it can work for arbitrary spatial sampling. Pen (1997) has implemented Salmon's method with FFT convolution, truncating the convolution window in such a way as to improve the sampling of long-wavelength waves in periodic boxes.

Non-Gaussian models are much more complicated. Not only do they require more information than the power spectrum, physical models also require costly computation. For example, topological defects induce matter density fluctuations from the time of their creation in the early universe all the way to the present day. The dynamics of defect formation and evolution are relativistic and fully nonlinear, requiring large-scale simulations to compute. Two classes of defect models have received the most attention: cosmic strings and global textures. The dynamic range requirements for cosmic string simulations starting before recombination and proceeding to low redshift are daunting (Allen & Shellard 1990, Bennett & Bouchet 1990). As a result, models for string initial conditions have been studied relatively little (e.g. Albrecht & Stebbins 1992a, b). Global textures are somewhat easier to simulate and have been included in cosmological structure formation simulations by Park et al (1991), Cen et al (1991), Gooding et al (1992).

Weinberg & Cole (1992) proposed a simple phenomenological class of non-Gaussian models: local nonlinear transformations of Gaussian random fields. In these models, unlike topological defects, the fluctuations are seeded in the early universe. They are easy to compute and provide useful comparisons against Gaussian models in order to assess effects of non-Gaussianity in simple control models.

Once the linear density fluctuation field has been specified at some initial time (at z ~ 100 for typical high-resolution simulations), dark matter particle positions and velocities must be obtained along with baryon density, velocity, and temperature fields. The standard approach for the dark matter is to displace equal-mass particles from a uniform Cartesian lattice using the Zel'dovich (1970) approximation (Doroshkevich et al 1980, Dekel 1982, Efstathiou et al 1985):

(6)

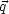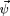where labels the unperturbed lattice position, D(t) is the growth factor of the linear growing mode, and f = d ln D / d ln a ^0.6 is its logarithmic growth rate (Peebles 1980). The irrotational (curl-free) displacement field is computed by solving the linearized continuity equation,

(7)

where (, t) is the relative density fluctuation. The displacement field is readily evaluated from Equation 7 using Fourier transform methods. The baryon velocity field is computed in a similar way, and the baryon temperature is generally initialized to the (redshift-dependent) microwave background temperature or to about 10⁴ K if the gas is ionized.

An alternative treatment of the dark matter sets the initial displacements to zero but gives the particles variable masses in proportion to (1 + ). The velocity for the linear growing mode is then proportional to the gravity field, = -(H f / 4 G ) 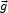. This method has been used by Warren et al (1992), who showed that it led to statistically indistinguishable results from the particle displacement method.

When particles are distributed initially on a lattice, the small-scale periodicity of the lattice persists visibly until virialization occurs, i.e. until particles fall into and orbit in gravitationally bound objects. To avoid this artificial pattern, particles may be perturbed from a random Poisson distribution instead of a lattice. However, the Poisson noise itself is a seed for gravitational instability, adding unwanted power to the desired spectrum. This noise may be eliminated by arranging the particles initially, before applying displacements, in a random "glass" state with very small gravitational forces. A gravitational glass is made by advancing particles from random positions using the opposite sign of gravity until they "freeze" in comoving coordinates (Baugh et al 1995, White 1996).

For some purposes, constraints may be imposed on the initial fluctuation field, e.g. that the simulation volume contain a rare high density peak on a scale ~ 10 h^-1 Mpc that will form a cluster of galaxies. Many independent realizations could be generated until one arises that closely satisfies the desired constraint by chance. An equivalent procedure is to use the method of constrained random fields. Bertschinger (1987) introduced an iterative but inefficient algorithm for constrained Gaussian random fields. Binney & Quinn (1991) showed that the sampling of peaks simplifies considerably when spherical coordinates are used, allowing a faster algorithm. A real breakthrough was made by Hoffman & Ribak (1991), who devised a relatively simple exact algorithm for sampling Gaussian random fields with arbitrary linear constraints [Salmon (1996) independently discovered the same trick]. The Hoffman-Ribak algorithm has been implemented in publicly available codes by van de Weygaert & Bertschinger (1996). Ganon & Hoffman (1993) have extended the algorithm to the case of many (hundreds or more) constraints specified on a regular lattice, in order to provide initial conditions for simulations matching the large-scale density or velocity fields of our own Universe. Sheth (1995) has extended the Hoffman-Ribak algorithm to local nonlinear transformations of Gaussian random fields.

The last ingredient that needs specification for most models is the matter power spectrum P(k), which is related (but not equal) to the mean squared amplitude of the Fourier transform of density fluctuations (Bertschinger 1992):

(8)

where _D is the Dirac delta function and angle brackets denote an ensemble average. [Each realization of () or (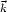), including the one that describes our own Universe at early times, is a random sample of an ensemble.] A factor of (2)³ may be included with P(k) in Equation 8 if an alternate Fourier transform convention is used. With the definition of Equation 8, the variance of density measured with a window function W (kR), when, for example, averaging over a sphere of radius R (equation 21.52 of Peebles 1993), is

(9)

In much (though not all) of the cosmology literature, d³k (Equation 9) is divided by (2)³, and P(k) is defined as larger by the same factor.

In Gaussian models, the post-recombination density field is the linear convolution of the primordial fluctuation field with a transfer function. (Slightly different transfer functions apply for CDM and baryons because of the finite Jeans length for baryons.) The power spectrum used to initialize simulations therefore generally takes the form

(10)

The primordial spectral slope n = 1 leads to curvature fluctuations of constant amplitude on all scales (Harrison 1970, Zel'dovich 1972). Because inflation occurred for only a finite duration, simple models predict a value slightly less than n = 1, and power-law inflation or other variants can readily produce "tilts" with 0.7 < n < 1.2 (Steinhardt 1995). The transfer function is normalized so that T(0) = 1. For CDM models, k²T(k) approaches a constant on small scales (e.g. Bardeen et al 1986).

The amplitude A of the primordial power spectrum is not specified by inflation or other models. Conventionally, it has been fixed one of two ways. The first is to require that the relative density fluctuations at redshift zero, averaged over a sphere of radius 8 h^-1 Mpc and computed using linear perturbation theory (i.e. using the simple linear transfer function T of Equation 10 with t_i set equal to the present time), equal the inverse of the "linear bias factor" b (defined and discussed below): ₈ = 1/b. The motivation for this choice is the observations that galaxy counts show fluctuations of unit amplitude in 8 h^-1 Mpc spheres (Davis & Peebles 1983) and the matter fluctuations are smaller by a factor b in the linear bias model. A more direct physical normalization has been possible since the measurement of microwave background anisotropy by the Cosmic Background Explorer (COBE) (Smoot et al 1992, Bunn & White 1997).

Transfer functions have been published by many workers; a useful early compendium was provided by Holtzman (1989). Such tables and fitting formulae have been superceded by publicly available codes that compute matter transfer functions and microwave background anisotropy (COSMICS by Ma & Bertschinger 1995, CMBFAST by Seljak & Zaldarriaga 1996). On a cautionary note, models with HDM (massive neutrinos) require more than just the transfer function; the HDM particles must be given a thermal distribution of momenta. For an accurate treatment, this distribution should itself be perturbed by gravitational effects (Ma & Bertschinger 1994a; see also Ma 1996).

Many papers have been written assessing structure formation models based on linear perturbation theory, the Press-Schechter theory (Press & Schechter 1974), and so on. Recent reviews of variants of CDM have been written by Liddle et al (1996a, b, c).

The roles of gravity, the transfer function, and linear and nonlinear evolution may be seen in Figure 2, which shows how the primordial scale-invariant fluctuations are modulated in several stages, to produce finally a tapestry of filaments, clusters, and voids.

Figure 2. Evolution of the potential and density in a simulation of a hot plus cold dark matter (HCDM) universe in a cube 50 h-1 Mpc across. Top left: scale-invariant gravitational potential fluctuations in the early universe. Top right: Post-recombination potential, showing the modulation by the transfer function. Bottom left: Post-recombination density fluctuations. Bottom right: Nonlinear density field at redshift 0, from a simulation with = 0.2 by Ma & Bertschinger (1994b).