Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

5.4. Radial Profiles of Dark Matter Halos

Numerical simulations of hierarchical models (Section 4) show that most of the mass is drawn into dense clumps by gravity. The dark matter components of these clumps are identified with extended dark matter halos around galaxies (Frenk et al 1985). N-body simulations have allowed cosmologists to address a straightforward question: What is the shape of dark matter halos formed by hierarchical clustering? This question is relevant observationally to the cusps of elliptical galaxies (e.g. Faber et al 1997) and the profiles of clusters of galaxies.

Gunn & Gott (1972), Fillmore & Goldreich (1984) presented analytical models for spherical "secondary" infall of collisionless matter onto a density peak in an expanding universe. Building on this work, Hoffman & Shaham (1985) proposed that virialized dark matter halos should have a power-law radial profile (r) r^-, where is related to the logarithmic slope n of the power spectrum on the scales of interest. For n < -1, the slope relevant on galaxy scales in plausible models, the prediction of the secondary infall model is = 2, corresponding to flat rotation curves such as those observed for the baryonic component of galaxies. For n > -1, the profiles steepen to = (9 + 3n) / (4 + n), corresponding to falling rotation curves.

The predictions of Hoffman & Shaham (1985) have been supported by many N-body simulations (e.g. Quinn et al 1986, Zurek et al 1988, Warren et al 1992, Crone et al 1994, Zaroubi et al 1996). However, high-resolution simulations (e.g. Frenk et al 1988) showed a steepening of the density profile with radius. Dubinski & Carlberg (1991) found that the halos formed in the CDM model have a logarithmic slope varying between 1 and 4, in good agreement with the Hernquist (1990) model. However, Navarro et al (1995, 1996) found instead a better fit to

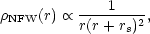(14)

where r_s is a scale radius. Their most surprising result was that this profile is universal for all hierarchical clustering models, regardless of the halo mass, the initial power spectrum, or cosmological parameters.

Navarro et al's results have been confirmed by Cole & Lacey (1996), Kravtsov et al (1997) and in higher-resolution simulations by Tormen et al (1997), Navarro et al (1997). The latter paper also shows that earlier work is, in fact, consistent with Equation 14. The characteristic density at r = r_s correlates with mass in a way that reproduces the trends of the Hoffman & Shaham (1985) model. However, in a still higher-resolution simulation, Fukushige & Makino (1997) found that the profile remains steeper than r^-1 to the limit of their resolution, and they attributed contrary results to two-body relaxation.

Why are the central profiles shallower than isothermal ( = 2)? Teyssier et al (1997) showed that when the Fillmore & Goldreich (1984) model is modified for gas, or dark matter with isotropic orbits, the limiting profile is = 1 instead of = 2. Alternatively, Evans & Collett (1997) examined the effect of diffusion driven by gravitational scattering and showed that the collisional Boltzmann equation of stellar dynamics has an attractor solution with = 4/3.

Halo shapes and angular momenta have also been studied with N-body simulations (e.g. Barnes & Efstathiou 1987, Dubinski & Carlberg 1991, Warren et al 1992). Numerically simulated dark matter halos are found to be generally triaxial and slowly rotating.