Annu. Rev. Astron. Astrophys. 1998. 36: 17-55 Copyright © 1998 by Annual Reviews. All rights reserved

2.2. Correlations

Here we consider correlations between observables other than the one just discussed between color and absolute magnitude. As stressed above, weak events like SN 1991bg are extreme in many of their properties, so when normal and weak SNe Ia are considered together, correlations are obvious. The more interesting issue is the extent to which correlations hold among normal SNe Ia. First we consider those among distance-independent observables.

It is clear that there is a correlation between spectrum and light-curve shape. Nugent et al (1995c) found that the spectroscopic observables R(Ca) and R(Si) correlate well with the light-curve decline rate m₁₅. Therefore the concept of a one-dimensional photometric/spectroscopic sequence is useful. The situation is not really that simple, though. For example, some events whose spectra look normal in the sense of Branch et al (1993) do not fit into a one-dimensional sequence in terms of the Si II blueshifts studied by Branch & van den Bergh (1993). SNe 1983G and 1984A had normal looking spectra but exceptionally high V₁₀(Si) values. Similarly, Hamuy et al (1996d) found that although in general their light-curve templates can be arranged in a one-dimensional sequence from slow to fast, some light curves having very similar initial decline rates show significant differences of detail. SN 1994D had an anomalously negative U - B color for its decline rate. And although SN 1992bc had a slower light curve than the spectroscopically peculiar SN 1991T, SN 1992bc had a normal looking spectrum. This and other evidence suggest that events like SN 1992bc may represent the "strong" end of the sequence of normals, while SN 1991T and similar events that have been discovered recently comprise a separate subgroup of powerful SNe Ia, which may be super-Chandrasekhar products of white-dwarf mergers in young populations (see Section 4.4).

Looking for correlations between B - V and other distance-independent observables is difficult because for all but the weak SNe Ia, the intrinsic B - V distribution is so strongly peaked near zero. The U - B color appears to cover more of a range than B - V (Schaefer 1995b) and to be correlated with other SN Ia properties (Branch et al 1997), but more U - B data are needed.

Spectra and light curves of SNe Ia also are correlated with the nature of the parent galaxies. On average, SNe Ia in red or early-type galaxies have lower values of V₁₀(Si) and faster light curves than those in late-type or blue galaxies (Hamuy et al 1995b, 1996a, Branch et al 1996b). The m₁₅ parameter is plotted against the color of the parent galaxy in Figure 6.

Figure 6. Light-curve decline rate m15 is plotted against parent galaxy color, corrected to face-on inclination. From Branch et al (1996b).

Now we consider correlations with absolute magnitude, which are the ones that are needed for improving on the standard-candle approach to H₀. Using Tully-Fisher (TF) and surface-brightness-fluctuation (SBF) distances for a sample of nine SNe Ia, including the peculiar SNe 1991T, 1986G, and 1991bg and the not-so-well-observed SN 1971I, Phillips (1993) found correlations between absolute magnitude (M_B, M_V, and M_I) an m₁₅. At one extreme SN 1991T was overluminous and somewhat slow to decline, and at the other SN 1991bg was extremely subluminous and quick to decline. The correlation was in the same sense as that proposed by Pskovskii (1977). Subsequently, the Calán-Tololo data on SNe Ia in the Hubble flow, for which the relative distances are more secure, showed that the correlation indicates considerable scatter among the dim, red, rapidly-declining events. After adopting a color cut to eliminate the three observationally red events in their sample, Hamuy et al (1996b) derived slopes d M_B / d m₁₅ = 0.78 ± 0.17, d M_V / d m₁₅ = 0.71 ± 0.14, and d M_I / d m₁₅ = 0.58 ± 0.13 (Figure 7). These slopes are much less steep than those that were obtained by Phillips (1993), yet definitely greater than zero. The Hubble diagram in V for the 26 non-red events, standardized by means of m₁₅, is shown in the bottom panel of Figure 4. When the correlations with m₁₅ were taken into account, the absolute-magnitude dispersions fell from those quoted in Section 2.1.3 to _obs(M_B) = 0.17, _obs(M_V) = 0.14, and _obs(M_I) = 0.13. Tripp (1997) found slopes that agreed well with those of Hamuy et al (1996b). In a straightforward but rigorous statistical analysis of the Calán-Tololo data, Tripp (1998) also introduced a linear dependence of absolute magnitude on B - V and found that d M_B / d m₁₅ falls to about 0.5; that B - V is more effective than m₁₅ in standardizing absolute magnitudes; and that the two-parameter corrections transform the Calán-Tololo sample into perfectly standardized candles insofar as can be measured with current techniques.

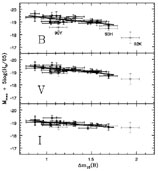Figure 7. Absolute magnitudes of the Calán-Tololo SNe Ia are plotted against light-curve decline parameter m15, with weighted linear least-square fits that exclude the observationally red SNe 1990Y, 1993H, and 1993K. From Hamuy et al (1996a).

Absolute magnitude also correlates with the spectroscopic indices discussed by Fisher et al (1995), Nugent et al (1995c), with parent-galaxy type (Hamuy et al 1996a, Saha et al 1997), and with parent-galaxy color (Hamuy et al 1995b, Branch et al 1996b). On average, normal SNe Ia in early-type or red galaxies appear to be dimmer by 0.2 or 0.3 mag than those in late-type or blue galaxies, and the absolute-magnitude dispersions of non-red SNe Ia in blue and in red galaxies, considered separately, are only about 0.2.

In an analysis that bears on many of the issues that have been discussed in this section, Riess et al (1995a, 1996a) have developed a formal statistical procedure to simultaneously estimate extinctions, relative luminosities, and relative distances from the shapes of light curves in the B, V, R, and I bands (multicolor light-curve shapes: MLCS). A training set of 9 SNe Ia with adopted distance and extinction estimates was used to establish a linear relationship between luminosities and light-curve shapes. Then individual extinctions, relative luminosities, and relative distances were inferred for an independent set of 20 Hubble-flow SNe Ia (including 10 from the Calán-Tololo survey) from their light curves. An attractive feature of MLCS is that it yields formal error estimates. The analysis gave results for various SN Ia properties such as relations between B - V, V - R, and R - I color curves and luminosity (Figure 8), and the dispersion in the MLCS distance moduli was found to be only 0.12 mag. These SN Ia properties are less directly "observational" than those discussed earlier in this section because they depend on the adopted properties of the training set, including TF and SBF relative distances, and on an assumed a priori probability distribution of the extinction. Of the 9 training-set events, 8 also were in the sample of 9 that was used by Phillips (1993) to derive magnitude-decline slopes that proved to be too steep, and the maximum-light B - V as parameterized by Riess et al (1996a) correlates with luminosity (Lira 1996) and m₁₅ (R Tripp, private communication) in ways that the Hubble-flow events of the Calán-Tololo sample do not. Assessing the consequences of changing the MLCS input data is not trivial; it will be interesting to see whether and how the results of MLCS change when the nearby training set is replaced by a subset of the Hubble-flow SNe Ia, whose relative distances will be more secure. See Riess et al (1998) for an interesting proposal to circumvent the labor of obtaining accurate multicolor light-curve shapes by combining the information carried in a single spectrum and a single-epoch measurement of B and V magnitudes to determine "snapshot" distances to SNe Ia.