The Cosmic Infrared Background - M.G. Hauser and E. Dwek

Annu. Rev. Astron. Astrophys. 2001. 39: 249-307
Copyright © 2001 by Annual Reviews. All rights reserved

4. COSMOLOGICAL AND ASTROPHYSICAL IMPLICATIONS

In this section, we discuss relatively direct implications of the EBL measurements. Models for the origin of the EBL are discussed elsewhere (Section 5).

4.1. Total EBL Energy

Important insights into the nature and evolution of the sources contributing to the EBL can be gained by examining its integrated energy and spectral energy distribution. Examination of Figure 5 suggests that the EBL spectrum has two maxima, with peaks at both optical and far-infrared wavelengths. This supports a picture of a background consisting largely of redshifted primary radiations at optical and near-infrared wavelengths, and reradiated thermal dust emission at far-infrared wavelengths. The existence of the long wavelength peak provides compelling evidence that the dominant luminosity sources are dusty.

We define I ident integ I d = integ I d ln as the frequency-integrated brightness of the cosmic background radiation. In the following tabulation, we give first the value of the integral (in nWm^-2 sr^-1) of the nominal EBL shown by the dashed line in Figure 5. We show in parentheses the range of values of the integral obtained using the upper and lower limits defined by the shaded area in Figure 5.

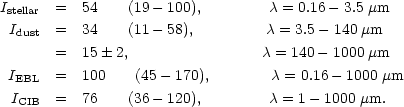$\begin{eqnarray*} I_{{\rm stellar}} & = & 54 \qquad (19-100),\ \qquad \qquad \lambda = 0.16-3.5~\mu{\rm m} \\ I_{{\rm dust}} & = & 34 \qquad (11-58),\ \ \qquad \qquad \lambda = 3.5-140~\mu{\rm m} \\ & = & 15\pm2,\ \ \qquad \qquad \qquad \qquad \lambda = 140-1000~\mu{\rm m} \\ I_{{\rm EBL}} & = & 100 \qquad (45-170), \qquad \qquad \lambda = 0.16-1000~\mu{\rm m} \\ I_{{\rm CIB}} & = & 76 \qquad (36-120),\ \qquad \qquad \lambda = 1-1000~\mu{\rm m}. \end{eqnarray*}$

The quoted uncertainty in the 140-1000 µm integral is 1 sigma . In presenting these integrated backgrounds, we have separated out the 3.5 to 140 µm range because there have been no direct detections of the dust emission in this spectral range.

Thermal emission from dust dominates the EBL spectrum at wavelengths longward of ~ 3.5 µm and constitutes about 48% of the nominal EBL. However, values ranging from 20% to 80% are consistent with the measurement uncertainties (Figure 5, shaded area). The nominal percentage is larger than the ~ 30% contribution of dust emission to the local (within ~ 75 h^-1 Mpc) luminosity density (Soifer & Neugebauer 1991), which suggests that the relative contribution of dust to the total energy output in the universe was higher in the past than at present. However, given the substantial uncertainty in the EBL measurements, the possibility that this fraction may have been constant or even lower in the past cannot be ruled out.

To compare the integrated EBL energy density with other cosmological energy budgets, it is useful to define the dimensionless radiative energy density, Omega _R, as

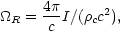$\begin{equation} \Omega_{R} = {4\pi \over c}I /(\rho_c c^2), \end{equation}$

(2)

where rho _c is the critical mass density of the universe, with

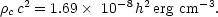$\begin{displaymath} \rho_c\,c^2 = 1.69 \times\ 10^{-8}\, h^2\, {\rm erg~cm^{-3}}. \end{displaymath}$

The energy density in the EBL is therefore a small fraction of the critical energy density,

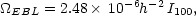$\begin{equation} \Omega_{EBL} = 2.48 \times\, 10^{-6} h^{-2}\,I_{100}, \end{equation}$

(3)

where I₁₀₀ ident I_EBL/(100 nW m^-2 sr^-1) lies in the range 0.45-1.7, as indicated above. The integrated CMB intensity, I_CMB, is 1000 nW m^-2 sr^-1 (Mather et al. 1999), or Omega _CMB = 2.48 × 10^-5 h^-2. Hence, the total EBL energy is also a small fraction of the radiant energy in the CMB:

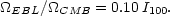$\begin{equation} \Omega_{EBL} / \Omega_{CMB} = 0.10\,I_{100}. \end{equation}$

(4)