The Cosmic Infrared Background - M.G. Hauser and E. Dwek

Annu. Rev. Astron. Astrophys. 2001. 39: 249-307
Copyright © 2001 by Annual Reviews. All rights reserved

4.2. Element Production and the Cosmic Star Formation Rate

The total EBL intensity is a measure of the bolometric energy output in the universe. It can be expressed as the integral of the comoving luminosity density (z) over redshift z (Dwek et al. 1998):

$\begin{eqnarray} I & = & \left({c\over 4\pi}\right)\ \int_0^{\infty} {\cal L}(z) \left|{dt\over dz}\right|{dz\over 1+z} \\ \nonumber & = & 9.63\times 10^{-8}\ h^{-1} \int_0^{\infty} \left[{{\cal L}(z)\over ({\rm L}_{\odot}\ {\rm Mpc}^{-3})}\right] H_0\left|{dt\over dz}\right|{dz\over 1+z} \qquad \nwat \end{eqnarray}$

(5)

where (Longair 1998; Chapter 7)

$\begin{equation} {\rm H}_0\left|dt/dz\right| = (1+z)^{-1}\left[(1+z)^2(1+\Omega_Mz)-z(2+z)\Omega_{\Lambda}\right]^{-1/2}, \end{equation}$

(6)

Omega _M ident rho _M / rho _c is the present mass density of the universe normalized to the critical density, and Omega ident Lambda / 3H²₀ is the dimensionless cosmological constant.

If we make the assumption that most of the EBL energy is produced by fusion of hydrogen, then the comoving luminosity density can be directly related to the cosmic star formation and element production rates. Fusion of hydrogen into heavier elements liberates 0.7% of the rest mass energy. The mass fraction of baryons in the form of hydrogen is denoted by X, and the decrement in this fraction due to nucleosynthesis in stars by Delta X. The luminosity density can therefore be expressed in terms of rho dot _X, the comoving mass production rate of helium and heavier elements:

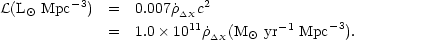$\begin{eqnarray} {\cal L}({\rm L}_{\odot}\ {\rm Mpc}^{-3}) & = & 0.007 \dot\rho_{_{\Delta X}}c^2 \\ \nonumber & = & 1.0\times10^{11}\dot\rho_{_{\Delta X}}({\rm M}_{\odot}\ {\rm yr}^{-1}\ {\rm Mpc}^{-3}). \end{eqnarray}$

(7)

The relation between and the comoving star formation rate, rho dot _*, depends on the stellar initial mass function (IMF) and is therefore not as robust as the relation between and the metal production rate. It is given by the convolution

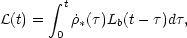$\begin{equation} {\cal L}(t) = \int_0^t \dot\rho_*(\tau) L_b(t-\tau)d\tau, \end{equation}$

(8)

where L_b(t) is the bolometric luminosity per unit mass of a stellar population of age t. For a constant star formation rate and a Salpeter IMF, n(M) propto M^-2.35 for 0.1 M < M < 120 M, where n(M) is the number of stars formed per unit mass M, the relation is given by

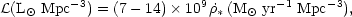$\begin{equation} {\cal L}({\rm L}_{\odot}\ {\rm Mpc}^{-3}) = (7-14)\times10^9\,\dot\rho_*\,({\rm M}_{\odot}\ {\rm yr}^{-1}\ {\rm Mpc}^{-3}), \end{equation}$

(9)

for populations of ages 10⁸ to 10¹⁰ years. If we assume a constant star formation rate over cosmic history, < rhodot _* >, then Equations 5 and 9 imply

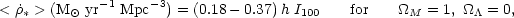$\begin{equation} <\dot\rho_*>({\rm M}_{\odot}\ {\rm yr}^{-1}\ {\rm Mpc}^{-3}) = (0.18-0.37)\,h\ I_{100} \qquad {\rm for} \qquad \Omega_M = 1,\ \Omega_{\Lambda} =0, \end{equation}$

(10)

similar to the result of Madau & Pozzetti (2000). In the local universe, the comoving star formation rate is only about 0.01 M yr^-1 Mpc^-3 (Madau et al. 1998). Thus, the observed intensity of the EBL suggests an average cosmic star formation rate that is 10-40 times higher than the rate at the present epoch.

To get a simple estimate of the amount of metals produced in the universe, we first assume that all metals were produced in a burst of star formation at redshift z_e and that all of the stellar energy was instantaneously released. The expression for I then simplifies to (Peebles 1993, Pagel 1997)

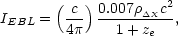$\begin{equation} I_{EBL} = \left({c\over 4\pi}\right){ 0.007 \rho_{_{\Delta X}}c^2\over 1+z_e}, \\ \nonumber \end{equation}$

(11)

where rho _X is the comoving mass density of consumed hydrogen atoms. We can write Delta X ident rho _X / rho _b = ( Omega _X / Omega _b), where rho _b and Omega _b are, respectively, the baryonic mass density and its value as a fraction of the critical mass density. The mass fraction of processed baryonic material can then be expressed in terms of the EBL intensity as

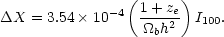$\begin{equation} \Delta X = 3.54\times10^{-4}\left({1+z_e\over \Omega_b h^2}\right) I_{100}.\end{equation}$

(12)

The value of Omega _b derived from Big Bang nucleosynthesis calculations is Omega _bh² = 0.0192 ± 0.0018 (Olive et al. 2000). For an emission redshift of z_e = 1, we get

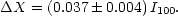$\begin{equation} \Delta X = (0.037\pm0.004)\,I_{100}. \end{equation}$

(13)

Hence, to get the observed EBL (I₁₀₀ = 0.45-1.7) with an instantaneous energy release at z_e = 1, one needs to convert 2%-6% of the nucleosynthetic baryon mass density into helium and heavier elements. The range of Delta X values is comparable to the solar value,

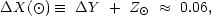$\begin{displaymath} \Delta X(\odot) \equiv\ \Delta Y\ +\ Z_{\odot}\ \approx\ 0.06, \end{displaymath}$

where Delta Y approx 0.04 is the difference between the solar (Y = 0.28) and the primordial (Y = 0.24) ⁴He mass fraction, and Z = 0.02 is the solar metallicity. Hence, the processing of the local ISM has been very similar to that of the average baryonic matter in the universe.

The instantaneous injection of energy is a considerably oversimplified description of reality. Even if all stars were formed instantaneously at some redshift z_e, their energy output would be spread over some time interval (Equation 8) that is at least as long as their main sequence lifetime (Madau & Pozzetti 2000). The EBL intensity will consequently fall off less steeply with increasing z_e than the (1 + z_e)^-1 cosmic expansion factor, lowering the fraction of processed baryonic mass density needed to produce the observed EBL intensity.

In reality, the cosmic star formation rate (CSFR) evolves with redshift. The EBL intensity can be used to test the validity of proposed star formation histories. For example, the CSFR determined from UV-optical observations of galaxies by Madau et al. (1998) implies a total extragalactic background in the 0.1 to 1000 µm range of ~ 30 nW m^-2 sr^-1 (Dwek et al. 1998). This increases to about 47 nW m^-2 sr^-1 for the CSFR of Steidel et al. (1999). Even the larger of these values is only marginally consistent with the allowed range of integrated EBL.

In general, the rate of star formation in individual galaxies can be inferred from a number of diagnostics based on the spectral energy distribution and energy output from young massive stars (Kennicutt 1998). Combining these diagnostics into a comprehensive picture of the global star formation history requires knowledge of the redshift of the galaxies being studied, and verification that no significant energy release has been overlooked by the use of a limited number of diagnostics. Hence, UV-optical observations of galaxies will a priori provide only a partial description of the true CSFR. Indeed, the discovery of dust-enshrouded luminous infrared galaxies in SCUBA 850 µm surveys and follow-up studies of the redshift distribution of these sources show that a significant fraction of the star formation activity at high redshift is taking place behind a veil of dust hidden from UV and optical observers (Hughes et al. 1998, Barger et al. 1998, 1999b, 2000, Lilly et al. 1999). Additional evidence suggesting that a significant fraction of the star formation occurred at redshifts z > 1-2 was provided by the iron abundance determinations in galaxy clusters with the Advanced Satellite for Cosmology and Astrophysics (ASCA) (Mushotzky & Lowenstein 1997, Renzini 1997), and by radio observations of galaxies (Haarsma et al. 2000) (Section 4.3). Revised estimates of the CSFR as a function of redshift that take into account some of the more recent developments are presented by Blain et al. (1999c), Haarsma et al. (2000).

Since a significant fraction of the energy released by stars is ultimately emitted at far-infrared wavelengths, it is interesting to examine what constraints can be set on the CSFR from the CIB detections alone. Equation 14 (Section 5) shows the relation between the EBL spectrum and the spectral luminosity density, ( , z), which, integrated over frequency, is proportional to the CSFR. The formal determination of the CSFR from the EBL is an inversion problem. Gispert et al. (2000) examined the possibility of determining the CSFR solely from the CIB measurements longward of 140 µm. To simplify the problem, they assumed that the intrinsic spectral luminosity, L(), of the galaxies that dominate the CIB does not evolve with time, so that ( , z) can be written as the product ( , z) = L() Phi (z), where Phi (z) is the comoving number density of galaxies. Gispert et al. used Monte Carlo simulations to explore a range of possible solutions for Phi (z) for various spectral shapes and intensities of L(). The method provided only weak constraints on the bolometric luminosity density (z) at z < 1 because of the lack of CIB data at wavelengths shorter than 140 µm. Their CSFR in the redshift range z approx 1-4 was found to be consistent with that inferred from galaxy observations (Steidel et al. 1999, Haarsma et al. 2000).

Gispert et al. (2000) concluded that the far-infrared region of the CIB strongly constrains the CSFR in the redshift range z approx 1-4. However, Dwek et al. (1998) showed that with different assumptions on the spectra of the CIB sources and the stellar initial mass function, one can obtain the observed CIB spectrum at wavelengths above 240 µm for two distinctly different star formation histories [see Section 5.2.2 and Figure 8]. The fact that different star formation histories provide equally good fits to the far-infrared CIB shows that only deep surveys that resolve the EBL into its individual sources can provide the definitive star formation history.

Galaxy counts obtained by the IRAS, ISO, and SCUBA observations have already provided useful constraints on the redshift evolution of the CSFR. The IRAS 60 µm counts suggest strong luminosity evolution propto (1 + z)^3.2±0.5 up to z approx 0.2 (Bertin et al. 1997). The ISO counts extended this evolutionary trend to z approx 1 (Puget et al. 1999, Altieri et al. 1999, Elbaz et al. 1999). The SCUBA observations of dust enshrouded sources at z geq 2 suggest that the CSFR at these redshifts should be moderately declining as (1 + z)^-1.1, or at most be constant. Otherwise, the integrated source light would exceed the submillimeter background (Dwek et al. 1998, Blain et al. 1999a, Takeuchi et al. 2001).